BOŞ YÜZEYLERDEN BUHARLAŞMA HESAPLAMASI

Genel

Su yüzeylerinden olan buharlaşma, aşağıdaki gibi değişik metodlar yoluyla belirlenebilir:

• Su bütçesi;
• Enerji bütçesi;
• Kütle transfer metodları;
• Kombinasyon metodları;
• Empirik formul.

Açıklanan metodların herhangi biri buharlaşmanın belirlenmesinde kullanılabilir. Genellikle, enerji bütçesi ve kütle transfer metodları için kullanılan araçlar oldukça pahalıdır ve gözlemleri sürdürebilmek için gereken maliyet oldukça önemlidir. Bu sebeplerden dolayı, buharlaşma havuzu kullanımı ve su bütçesi metodu yaygın olarak kullanılmaktadır. Havuz metodu, en az pahalı olandır ve yıllık buharlaşmanın iyi hesaplanmasını sağlar. Seçilen herhangi bir yaklaşım, hassasiyet gereken derecelere bağımlıdır. Su bütçesi ve enerji bütçesi parametrelerin değerlendirmek için yeteneği geliştirdikçe, bu aynı zamanda tahmin edilen buharlaşma hesaplanmasını sonuçlandıracaktır.

Su bütçesi

Metod, süreklilik eşitliğine dayanır ve buharlaşma hesaplamaları amacı için faydalı olabilir:

E = I – O – ΔS (4.2)

• E = buharlaşma,
• I = içeri akış,
• O = dışarı akış
• ΔS = depodaki değişim

Sırasıyla yeryüzeyinin belirten 4.2’de vektör çizgilerinin altında ve üstünde oluşan denklemdeki değişik bileşenlere s ve g eklerinin katılması yoluyla, eşitlik şu şekilde ifade edilebilir:

E^s = P + R¹ – R² – R^g – T^s – F – ΔS^s (4.3)

• Es = rezervuar buharlaşması,
• P = yağış,
• R¹ = rezervuar içine gelen yüzey akışı,
• R² = rezervuardan giden yüzey akışı,
• R^g = yer altı suyu akışı,
• T^s = Terleme kaybı,
• F = sızma (veya sızıntı)
• ΔS^s = depolama değişimi.

Sızıntının net transferi (Rg – F) = Os ve terleme terimi Ts sıfıra eşitse, o zaman 4.3 eşitliği yeniden yazılabilir:

E^s = P + R¹ – R² + O^s – ΔS^s (4.4)

Bütün terimler, bir haftadan az olmamak üzere çalışılan zaman periyodu için hacimsel birimlerdir. Teoride basit olmasının avantajına rağmen 4.4 eşitliğinde kullanılan parametrelerin ölçümündeki hatalardaki dezavantaja sahip olan su bütçesi metodu, buharlaşma miktarı hesaplamasında doğrudan yansıtır. Bundan dolayı, buharlaşma hesabı gerçek miktarın yüzde ±5’i civarında olması bekleniyorsa bu metodun bir aydan kısa olan zaman periyoduna uygulanması tavsiye edilmez.

Belki de değerlendirilecek en zor parametre sızmadır F. Bu bileşen göl yatağının hidrolik iletkenliği ve hidrolik gradyanının bilinmesiyle hesaplanabilir. Ancak yine de buharlaşmanın belirlenmesinde kullanılan su bütçesi hesabı, buharlaşma miktarı karşılaştırmalarında sızmanın göz ardı edildiği su geçirmez göllere oranla uygulandığında çok başarılı sonuçlar ortaya koyacağı kabul edilmiştir.

ΔS^s’yi değerlendirmek için, göl için kesin bir alan-kapasite eğrisi olmalıdır. Bu verilere rağmen, depolama bileşeni, su bütçesinde bir hatayı ortaya koyabilir. Bununla beraber, depolama bileşeni ihmal edilirse, su bütçesi yıllık döngüde yararlı olmayacaktır.

Herhangi boş bir yüzeyden olan buharlaşma hesabı için su bütçesi metodu kullanmak teorik olarak mümkün olmasına rağmen, bunu yapmak değişik parametrelerin ölçümündeki hataların etkisi sebebiyle kullanışsızdır. Bu metodla hesaplanan buharlaşma artıktır ve bundan dolayı diğer parametrelere nispeten küçük ise hata dikkate değer ölçüde sorun olabilir.

Özet olarak, metod özellikle zaman periyodu kısa olduğu çoğu şartlar altında zor ve hatalı sonuç verir. Ölçümdeki çoğu zor parametrenin bazıları depo, sızma, yer altı su akışı ve adveksiyon akışlarında değişir.

Enerji bütçesi

Enerji bütçesi metodu, enerji teriminde yazılan bir süreklilik eşitliğinin uygulamasını tanımlar. Örneğin New Mexico’da (Gunaji, 1968) Elephant Butte Rezervuarındaki göller ve okyanuslardan olan buharlaşma hesaplamalarında çalıştırılır. Denklem sistemde depolanan enerji miktarı yoluyla dengelenen gelen ve giden enerjiyi hesaba katar. Enerji bütçesini kullanan buharlaşma hesaplarının doğruluğu, ölçülen verinin hatasızlığına ve güvenilirliğine yüksek derecede bağlıdır. İyi şartlar altında, kış ayları için %20, yaz periyodu için %10 ortalama hata beklenebilir.

Bir göl için enerji bütçesi denklemi (Viessman ve diğerleri, 1989) şu şekilde yazılabilir:

Q⁰ = Q^s – Q^r + Q^a – Q^ar – Q^bs + Q^v – Q^e – Q^h – Q^w (4.5)

• Q⁰ = Su tarafından depolanan enerjideki artış,
• Q^s = Su yüzeyindeki solar radyasyon,
• Q^r = Yansıtılan solar radyasyonu,
• Q^a = Atmosferden gelen uzundalga radyasyonu,
• Q^ar = Yansıtılan uzun dalga radyasyonu,
• Q^bs = Su tarafından yayılan uzun dalga radyasyonu,
• Q^v = Su kütlesindeki net enerji adveksiyonu(gelen ve giden suyun net enerji içeriği),
• Q^e = Buharlaşmada kullanılan enerji,
• Q^h = Hissedilir ısı olarak su kütlesinden iletilen enerji ve
• Q^w = Buharlaşan sudan olan enerji adveksiyonu.

4.5 denklemindeki bütün terimler, her gün için metre karedeki watt’dır (W m–2gun). Kimyasal değişiklikler ve biyolojil işlemler neticesinde ortaya çıkan ısınma su yüzeyinde oluşan ısı transgeri gibi göz ardı edilmiştir. Ayrıca termal enerjinin kinetik enerjiye dönüşümü dahil edilmemiştir. Bu faktörler, büyük rezervuarlar göz önüne alındığında bütçedeki diğer terimlere kıyasla genellikle çok küçüktür.

Sonuç olarak bunların eksikliği sonuçların güvenilirliği açısından küçük etkiye sahiptir. Enerji bütçesi denklemindeki değişik terimlerin her biri bilinen bağıntılardan hesaplanabilir veya doğrudan ölçülebilir.

Her terimin değerlendirilmesinde kullanılan prosedür aşağıda tanımlanmıştır. Ölçülebilen 4.5 denklemindeki terimler Q^s, Q^r ve Q^a‘dır ve net radyasyon dengesi:

R^f = Q^s – Q^sr + Q^a – Q^ar – Q^bs (4.6)

Yukarıdaki bütün değerler W m–2’dir.

Yukarıda bahsedilen elemanların ölçüm teknikleri ve enstrümanlarının detaylı tanımlamaları 4.1.3, 4.1.4 ve 4.1.5 veya “Guide to Meteorological Instruments and Methodsof Observation (WMO-No. 8)”da bulunabilir.

Yansıltılan uzun dalga radyasyonu (Q^ar) su yüzeyinden alınan uzun dalga radyasyonunun %3’ü kadar alınabilir.

Su (Q^bs) tarafından yayılan uzun dalga radyasyonu su için 0.970 olan yayılım faktörü ile siyah-gövde radyasyonu için Stefan–Boltzmann kanununa uygun olarak hesaplanır. Su yüzeyinden yayılan radyasyon hesaplama eşitliği ise:

Q^bs = 0.97δθ4 (4.7)

Q^bs = W m_–2 olarak su yüzeyinden yayılan radyasyonu, δ Stefan-Boltzmann sabiti (5.67 x 10–8 W m^–2 °K^–4), ve θ °K olarak su yüzeyi sıcaklığıdır. Hesaplama amaçları için rezervuarın merkez noktası civarında kaydedilen ortalama su yüzeyi sıcaklığı her bir çalışma periyodu boyunca belirlenir. Sıcaklık °K’e dönüştürülür ve su yüzeyinden yayılan ortalama radyasyon W m–2 biriminde çalışma periyodu için hesaplanır.

Belirli bir tarih için rezervuardaki suyun hacminin termal enerjisi o tarihte yapılan sıcaklık tetkikinden hesaplanır. 0.1°C hassasiyette olması gereken bu sıcaklık ölçümleri genellikle iki haftada veya bir aylık aralıklarda yapılır. Rezervuar yüzeyden dibe kadar birçok seviyeye bölünebilir. Her bir tabakadaki suyun hacmi basamak-hacim ilişkisinden belirlenir. Belirli bir tabakada yapılan bütün sıcaklık gözlemleri su hacmi için ortalama sıcaklık elde etmek için ortalaması alınır.

Sıcaklık (0°C taban sıcaklık olarak göz önüne alındığında) ve hacim ürünlerinin toplamı belirli bir tarih için toplam enerjiyi verecektir. Yoğunluk ve spesifik ısı rezervuarda oluşan sıcaklıkların aralığı için bütünlük olarak göz önüne alınır. Buharlaşmada kullanılan enerjiyi belirlemek için rezervuara giren veya çıkan suyun hacmindeki enerji adveksiyonundan elde edilen enerji stoğundaki Qe değişimleri değerlendirmeye alınmalıdır. Tekrardan, 0°C taban sıcaklığı genellikle bu hacimlerdeki enerji miktarının hesaplanmasında seçilir. Bu sıcaklıklar akış oranıyla sıcaklığın değişimine bağlı gözlem veya kayıtlar (4.1.3) yoluyla belirlenir. Suyun sıcaklığı akış oranıyla değişiyorsa, hacimdeki ortlama sıcaklık akış oranına bağlı olarak ağırlıklandırılmalıdır. Depodaki ve net sızma sıcaklıkları ortalama yıllık hava sıcaklığına eşit olarak göz önüne alınır. Bu varsayım kuşkusuz hataya konu olur fakat yüzeye su girdisi su bütçesinde büyük bir kısmı oluşturuyorsa ciddi olarak değerlenidirilmez.

Yağış su bütçesinde önemli bir yer kaplıyorsa o zaman bu su hacminin enerjisi hesaplamaya katılmalıdır. Düşen yağışın sıcaklığı yağmur zamanındaki ıslak hazne sıcaklığı olarak farzedilir. Bu hacmin her birisi için enerji hesaplamalarında, santimetre-gram-saniye birimleri kullanılır ve yoğunluk ve spesifik ısı bu hacimde oluşan sıcaklık aralığında bütün olarak göz önüne alınır. Sıcaklık zaman hacmi ürünleri joule olarak (net enerji adveksiyonu, Qv) her bir hacmin enerji toplamını verecektir. Çalışma periyodunun başında ve sonunda yapılan termal tetkikler için depolanan suyun hesaplanan enerjisinin arasındaki fark enerjideki (Q0) değişimi belirler.

Kısmen veya tamamen karla kaplı alanlar olduğu zamanlarda enerji bütçesi zaman zaman uygun sonuçlar vermeyebilir çünkü yansıtılan solar radyasyonu, buz yüzey sıcaklığını ve buz tabakasının alansal yüksekliğini ölçmek zordur. Enerji bütçesine dayalı günlük buharlaşma hesaplamaları bir çok çalışmada mümkün değildir çünkü bu gibi kısa periyotlar için depolanan enerjideki değişimin düzgün belirlenmesi kullanışsızdır.

Bir hafta veya daha uzun periyotlar daha memnuniyet verici ölçümler sağlaması muhtemeldir. Enerji bütçesi yaklaşımını kullanarak, ölçümler için gereken hassasiyetin bütün değişkenler için aynı olmadığı gösterilmiştir. Örneğin yansıtılan solar enerjinin ölçümünde %10’luk hatalar aylık buharlaşma hesaplarında %1-5 hataya sebep olurken, %2 kadar küçük gelen uzun dalga radyasyonu ölçümündeki hatalar aylık buharlaşma hesaplamalarında %3-15’lik hataya neden olur. 4.5 denklemindeki buharlaşmanın belirlenmesi için çoğunlukla aşağıdaki eşitlik kullanılır;

B = Bowen oranı (Bowen, 1926) ve:

C^p = 4186.8 J/kg°C’ye eşit olan su spesifik sıcaklığı (cal/g°C),

T^e = Buharlaşan suyun sıcaklığı (°C) ;

T^b = Genellikle 0°C olarak alınan taban sıcaklığı

L = 2260 kJ/kg’a eşit olan buharlaşma gizli sıcaklığı (cal/g).

4.5 denklemindeki bu ifadelerin getirilmesi ve Q^e için çözülmesiy ile şunu elde ederiz:

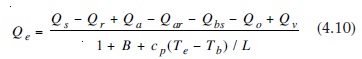
Birim zaman için buharlaşan suyun derinliğini belirlemek için aşağıdaki ifade kullanılabilir:

E = buharlaşma (m sec_–1) ve ρ= buharlaşan suyun kütle yoğunluğu (kg m_–3).

Böylece enerji bütçesi denklemi şu hale dönüşür:

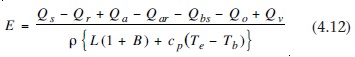
Aşağıdaki denklemle Bowen katsayısı hesaplanabilir:

• p = Atmosferik basınç (mb),
• T^o = Su yüzeyi sıcaklığı (°C);
• T^a = Hava sıcaklığı (°C),
• e^o = su yüzeyi sıcklığındaki yoğuşam buhar basıncı (mb)
• e^a = havanın buhar basıncı (mb).

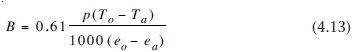
Bu ifade direkt ölçüme uygun olmayan hissedilir ısı terimi değerlendirmesi problemini önler. Buharlşama hesabı için kullanılan birçok parametrenin uzaktan algılanması, daha önce 4.1.3’de bahsedilen dünya yüzeyinden yansıtılan veya yayılan belirli bir dalga bandındaki elektromanyetik radyasyonun ölçülmesi yoluyla yapılır.

Enerji bütçesi yaklaşımının kullanılabilirliği

Aşağıda anlatılan noktalar boş yüzeylerden buharlaşma hesaplamaları için enerji bütçesi yaklaşımına uygulamak için ilk olarak geçerliliği kabul edilmiştir:

(a) Gölün dibinden ısı akışı hesaba katılmamıştır. Bununla beraber sığ göller için bu önemlidir;

(b) Bowen oranı Qh‘ın yeteri doğrulukta hesaplanmasını sağlamak için kabul edilmiştir.

(c) Yaklaşım havanın stabilitesi, radyatif yayınıma bağlı etkileri ihmal eder;

(d) Yaklaşımın uygulanabilirliği advektif enerji bileşenlerini değerlendirmeya dayanaktır.

Kütle-transferi metodu

Kütle transferi yaklaşımı, adı üzerinde su yüzeyinden atmosfere transfer edilen su buharı kütlesinin belirlenmesine dayanır. Bunu daha iyi anlamak için hava hareketi fiziğine bakış tartışılacaktır. Hava, su yüzeyleri veya kara üzerinden geçerken aşağı atmosferdeki hava kalınlığı üç tabakaya ayrılabilir:

(a) yüzey yakınındaki laminer tabaka;

(b) turbulans tabakası;

(c) sürtünme etkilerinin dışındaki tabaka.

Hava akışının düzgün olduğu laminar tabaka, kalınlığı milimetredir. Bu tabakada sıcaklık, nem ve rüzgar hızı hemen hemen yükseklikle lineer olarak değişir ve ısı transferi, su buharı ve momentum moleküler işlemlerdir.

Başta gelen türbülans tabakası, türbülans seviyesine dayanan birçok metre kalınlıkta olabilir. Bu tabakada, sıcaklık, nem ve rüzgar hızı yaklaşık olarak yüksekliğin logaritması ile lineer olarak değişir ve bu tabaka boyunca ısı transferi, buhar ve momentum türbülans işlemidir. Kütle-transferi yaklaşımı, buharlaşma ve buhar basıncı arasındaki ilişkiyi veren Dalton’un aerodinamik kanununa dayanır.

E = k (e^s – e^a) (4.14)

E = direkt buharlaşma, k = bir katsayıdır ve rüzgar hızı, atmosferik basınç ve diğer faktörlere dayanır, e^s ve e^a = Havanın buhar basıncı ve su yüzeyi sıcaklığına tekabül eden buharlaşma buhar basıncı. Ortalama günlük sıcaklık ve nispi nem ortalama buhar basıncı e^a ve ortalama yoğuşma noksanlığı (e^s – e^a) belirlenmesinde kullanılabilir. 4.14 denklemi Harbeck ve Meyers (1970) tarafından teklif edilmiştir.

Aerodinamik ve enerji dengesi metodlarının kombinasyonu

Meteorolojik faktörlerden göl buharlaşması hesaplaması için en yaygın kullanılan metod aerodinamik ve enerji-dengesi denkleminin kombinasyonuna dayanır:

Eⁱ = serbest su yüzeyinden hesaplanan buharlaşma

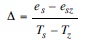
Yandaki ifade, Brutsaert’de (1982, Şekil 10) T^z‘e karşı γ/Δ tablolanan herhangi bir sıcaklıktaki θa yoğuşma buhar basıncı eğimi, Rn = net radyasyon, γ ıslak ve kuru hazne pisikrometre denklemindeki sabit ve Ea = 4.14 denkleminde açıklandığı gibidir. °C için pisikrometre sabiti Bowen oranı sabitinin aynısıdır ve 1000 mb’daki değeri 0.61’dir. Net radyasyon Rn (MJ m–2 gün) aşağıdaki formülle hesaplanabilir:

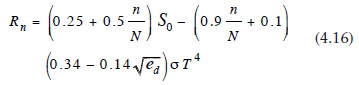
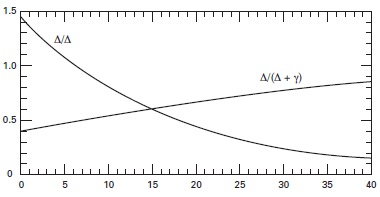
Şekil 10. γ/Δ’nın Sıcaklık bağımlılığı ve 1000 mb’daki Δ/Δ+γ) Brutsaert (1982)

n/N = mümkün güneşlenme süresinin gerçekleşene oranı, S⁰ = dünyanın dışındaki radyasyon (MJ m–2 gün), e^d = civa yüksekliği (mm) olarak havanın aktüel buhar basıncı, δ= Stefan–Boltzmann sabiti, ayrıca mm day–1 ölçeğinde eşdeğer buharlaşma olarak tanımlanır, ve T = Kelvin olarak ortalama hava sıcaklığı (mutlak).

Yukarıdaki eşitliği kullanmak gerekli olsa da, solar ve uzun dalga radyasyonunun ölçülmüş değerlerinin kullanılması tercih edilir.

Atmosfere olan buharlaşma, benzer bir yaklaşım Kohler ve diğerleri (1959) tarafından kullanıldı ve bağlantının grafiksel sunumu Şekil I.4.4’de gösterilmiştir. Sınıf A havuzundaki anemometre yüksekliğinde solar radyasyon, hava sıcaklığı, çiğ noktası ve hava hareketinin meteorolojik gözlemleri bu tekniğin uygulaması için gerekir. Solar radyasyon gözlemlerinin eksikliğinde, radyasyon mümkün olan güneşlenme veya bulut kapalılığı verisinin oranından hesaplanabilir. Bu metodla kısa periyotlar için hesaplanan göl buharlaşması, göle enerji adveksiyonu yokken veya azken çok sık bir şekilde göllere uygulanabilir. İçeriye veya dışarıya doğru akımlara bağlı önemli adveksiyonun koşulları ve derin göller için, enerji depolamasındaki değişim, hesaplanan göl buharlaşması veya net adveksiyon enerjisini düzeltmek gerekir. Bu terimler, 4.2.3’deki enerji bütçesi metodu altında açıklanmaktadır. Bununla beraber enerji depolamasındaki değişim ve adveksiyon enerjisinin hepsi buharlaşma için kullanılamaz. Buharlaşma için kullanılan bu enerjinin payı Şekil I.4.5’de gösterildiği gibi bir bağıntıdan elde edilir. Su yüzeyinin 4 metre üzerinde hava hareketi ve su yüzeyi sıcaklığı gözlemleri, bu bağıntının uygulaması için gerekir. Enerji adveksiyonu ve depolama faktörlerinden bir değerlendirme yapılrsa haftalık veya aylık göl buharlaşmasının güvenilir hesaplamaları bu yaklaşım yoluyla elde edilebilir.

Havuz ölçümlerinden ekstrapolasyon

Zeminin üzerine veya içine koyulmuş havuzlardan olan buharlaşma havuzun karaktersitiklerinden etkilenir. Gömülmüş havuzlar tespit edilemeyen sızıntı, su yüzeyinde biriken parçalar ve geniş bir gölden farklı toprakla sınır koşulları konu edilmelidir. Zemin üzerine yerleştirilen havuzlar kenarlar arasındaki sıcaklık değişimi ve göllerde oluşmayan diğer etkileri ortaya çıkarır. Yüzen havuzların içine ve dışına su sıçraması oluşur ve kurulması ve işletilmesi pahalıdır.

Havuzlar göllerden daha az ısı kapasitesine sahiptir ve mevsimde erken oluşan havuz buharlaşmasıyla buharlaşmanın farklı bir yıllık döngüsünü tecrübe etmeye eğilimlidir. Yıllık göl buharlaşmasının güvenilir hesaplamaları, uygun havuz-göl sabiti yoluyla yıllık havuz buharlaşmasının çarpımıyla elde edilebilir. Yıllık bazda göle transfer olan herhangi enerjinin ısı depolamasındaki değişim yoluyla dengelendiği kabul edilirse, bu hesaplamalar güvenilir olacaktır. Belirli bir havuz için havuz-göl katsayısı aktüel göl buharlaşmasıyla karşılaştırılarak veya bir gölü (çapı 4 metre veya fazla zemin içine gömülmüş havuzlar) simüle edecek kadar yeterli büyüklükte bir havuzla kıyaslama yaparak belirlenir. Belirli bir havuz için katsayı, kurak veya nemli şartlardan farklı klimatolojik rejim üzerinde bir dereceye bağlıdır. Buharlaşma havuzunun göl buharlaşmasında geçerli bir indeks olarak hizmet etmesi için havuzun çıkarılması gölün çevresel etkilerini önlemelidir.

Bu tür bir açıkta kalma durumu göl yakınında olabilir fakat hakim rüzgar yönüne doğru olmalıdır. Havuz katsayısının iklimsel değişiminin belirlenmesinde ki metodlardan biri değişik koşullar altında geniş havuzlarla alansal karşılaştırmalar yapmaktır. Bu metod GGI-3000 ve 20-m2 tanklarıyla bağımsız devletlerin genel durumuna göre uygulanır.

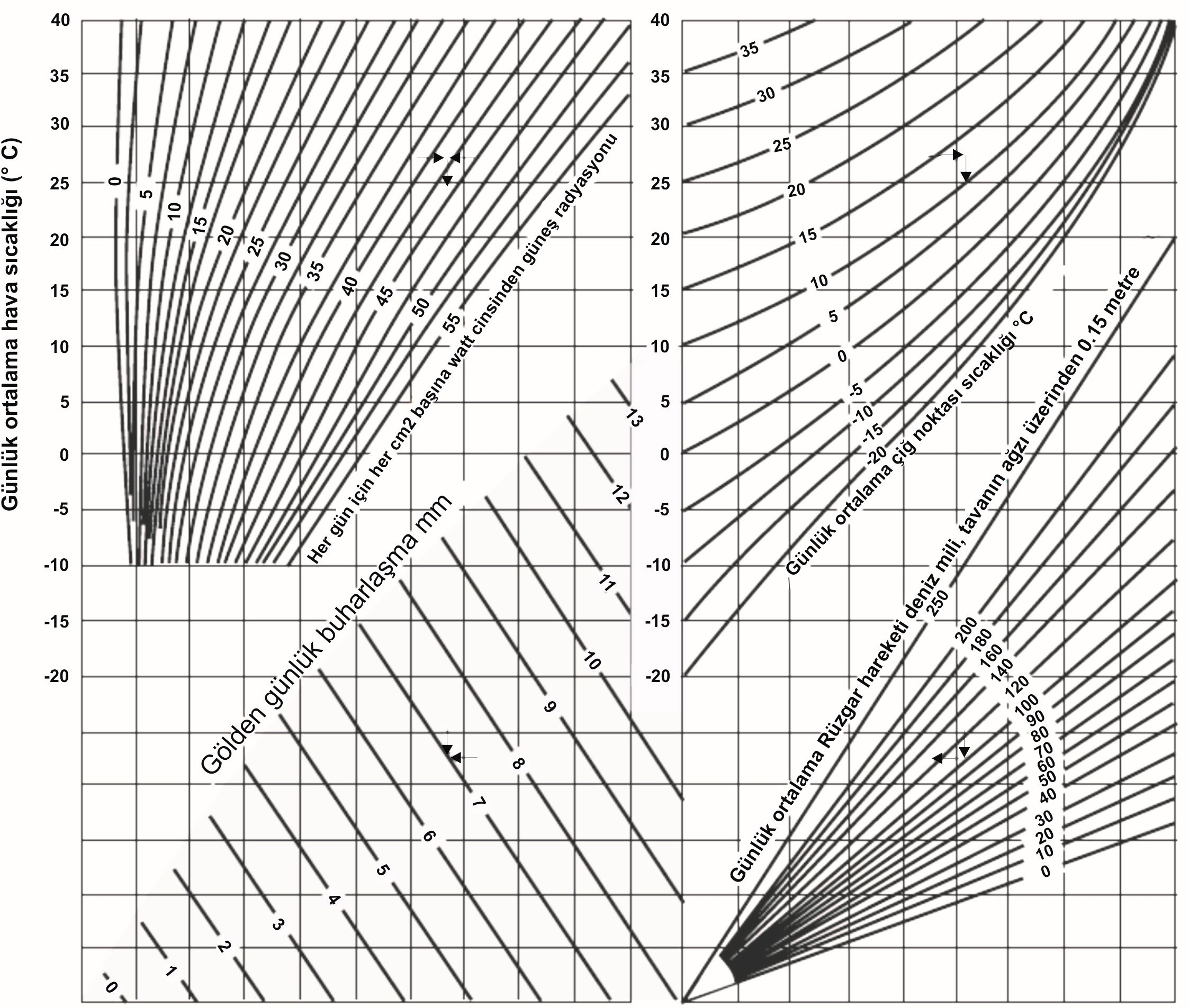
Şekil 4. Göl–buharlaşma ilişkisi
Not: Uluslar arası Pireliometrik Ölçek, 1 Temmuz 1957’de Birleşik Devletler’de kullanılmaya başladı, bundan önce elde edilenden %2 daha az değerleri sağladı. Bundan dolayı, 1 Temmuz 1957’den sonraki verilere dayalı hesaplamalarda %2 radyasyon değerleri atmıştır.

Havuz-göl katsayısı GGI-3000 için 0.75 ile 1.00 arasında elde edildi. Aylık ortalama buharlaşma hesabınde yüzen bir GGI-3000 buharlaşma havuzu katsayısı aşağıdaki denklemle hesaplanır.

eo = suyun yüzey sıcaklığından hesaplanan hPa olarak ortalama aylık buhar basıncı, e’o = yüzen GGI-3000 havuzundaki su yüzeyi sıcaklığından hesaplanan hPa olarak ortalama aylık buhar basıncı, e200 = su yüzyinden 200 cm yukarıda hPa olarak aylık ortalama buhar basıncı, β= su kütlesi alanı için düzeltme faktörü, ve γ = kıyıdan havuza doğru ortalama rüzgar yönü boyunca mesafeye (l) bağlı faktör (feç).

Oran, β/γ, havuz kıyıdan 500 metre uzkalığa kadar bir mesafeye yerleştirildiğinde tundra, orman ve orman-step bölgelerinde yer alan su kütleleri için belirlenir. Diğer durumlarda oran 1’e eşit olarak kabul edilir. Yaklaşık yuvarlak veya kare şeklindeki su kütleleri için β tablo I.4.1’de kullanılarak su yüzeyi alanları için belirlenir.

Tablo 1. β'nin Belirlenmesi

Su Kütlesinin Alanı (km2	0.01	0.05	0.1	0.5	1.0	2.0	5.0
Düzeltme Faktörü β	1,03	1.08	1.11	1.18	1.21	1.23	1.26

Düzensiz şekle (ada ve körfez) sahip su kütleleri için pergelin 8 noktasından yüzde olarak rüzgar yönünün frekansıyla ağırlıklı, ortalama mesafeye (l)eşit bir çaplı daire olarak kabul edilir. Ağırlıklı mesafe 4.18 denklemiyle hesaplanır:

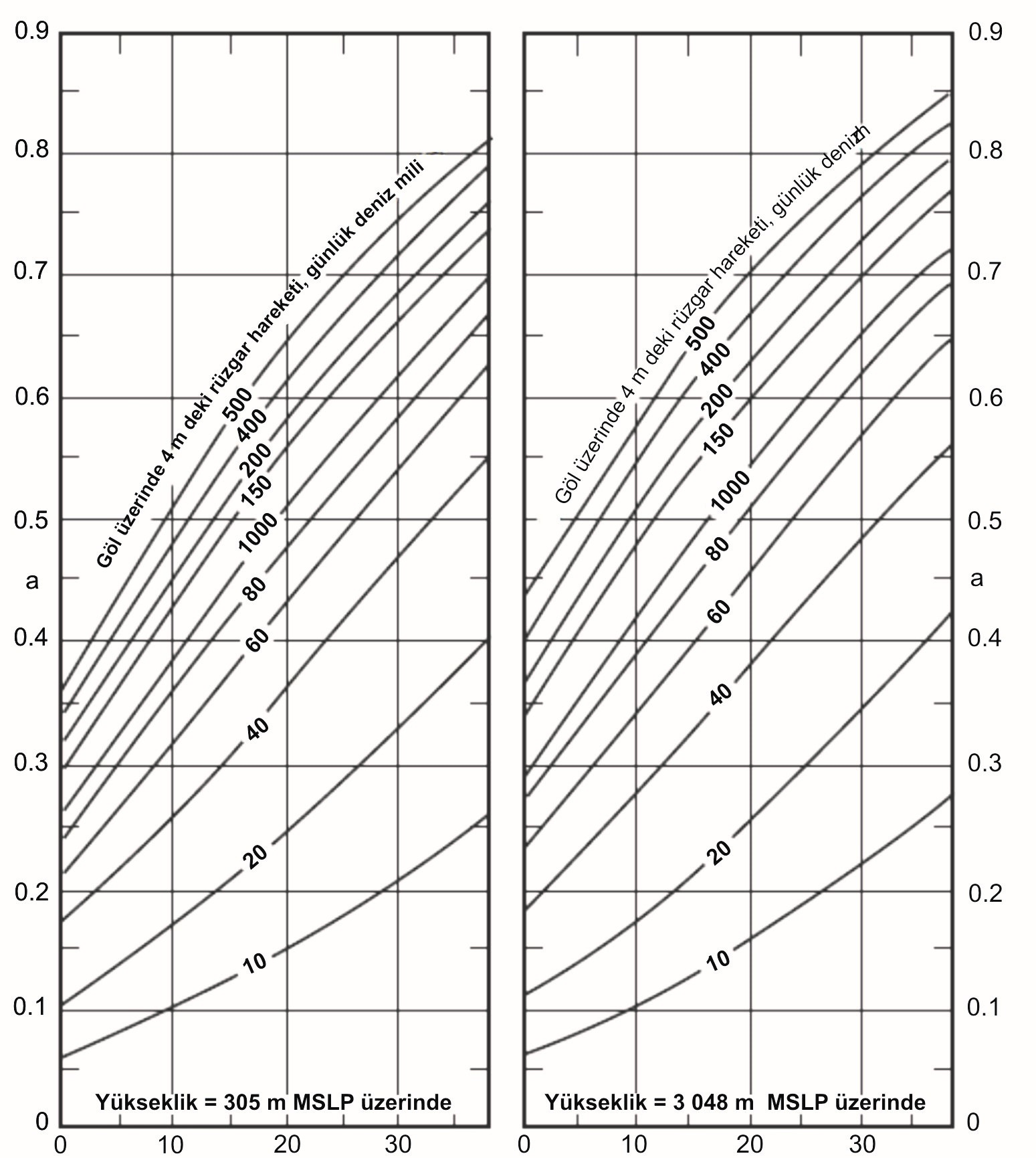
Şekil 5. Buharlaşma için kullanılan göldeki adveksiyon enerjisinin payı

Nⁱ = yüzde olarak 8 noktadaki rüzgar yönün frekansı; Şekil 6’dan γ hesaplanabilir.

Diğer bir metod, kenarlar ve dipden ısı kazanım veya kaybının buharlaşma havuzundan düzeltilmesidir. Bu metoda örnek A sınıfı buharlaşma havuzundan elde edilen veriyi kullanrak buharlaşma hesaplama tekniğidir. Nemli mevsim ve iklimlerde, havuz suyu sıcaklığı hava sıcaklığından yüksektir ve havuz katsayısı 0.80 veya yüksek olabilir. Yağışsız mevsim ve kurak alanlarda havuz suyu sıcaklığıhava sıcaklığından düşüktür ve katsayı 0.60 veya daha az olabilir. Su ve hava sıcaklığı eşitken 0.70 katsayısı uygulanabilir kabul edilir. Isı kazanım veya kaybı için A tipi buharlaşma havuzu düzeltmesi yoluyla göl buharlaşması hesabı için olan bağlantı şekil I.4.7 ve şekil I.4.8’de gösterilmiştir. Yükseklikle rüzgar değişiminin öneminden dolayı, standart cihaz yüksekliği A tipi istasyonun asli gereksinimidir.

Havuz metoduyla göl buharlaşmasının kısa periyotlu hesaplamalrını elde etmek için, göle net enerji adveksiyonunu ve 4.2.3’de tanımlanan enerji depolamasındaki değişimi değerlendirmek gerekir. Diğer meteorolojik verilerin yokluğunda alternatif veri kaynağı olarak rezervuar veya göl yakınında havuz buharlaşması yapmak ve enerji bütçesi ve aerodinamik metodlarla yapılan hesaplamaları verifikasyon yapmak faydalıdır.

Empirik formül

Enerji bütçesi ve kütle transfer metodları, teorik olmasına rağmen bir çok çalışma için henüz hazır olmayan veri gerektirir. Dahası birçok durumda göl enstrümanlarından elde edilen veri ekonomik olmasına rağmen kuşkuludur. Böylece birisinin buharlaşma tahminlerini elde etmek için empirik formüllerin kullanımını yapmak zorundadır. Buharlaşma tahminlerini elde etmekte kullanılan birçok empirik formül, enerji bütçesi veya kütle transferi metoduyla (Mutreja, 1986) geliştirilmiştir.

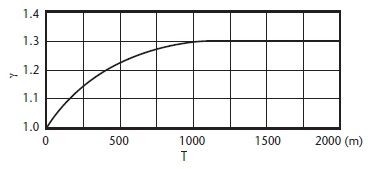
Şekil 6. γ faktörü ve T ilişkisi

Bununla beraber, bir çok eşitlik 4.14 denkleminde verildiği gibi basit aerodinamik eşitliğe dayanır. Göl yüzeylerinden olan buharlaşmanın tahmini için kullanılan bu empirik formüllerin çok kullanılan birkaç tanesi aşağıda verilmiştir:

Penman formülü, Birleşik Krallık – küçük tank (Penman, 1948)

E(cm gün_–1) = 0.89 (1 + 0.15U²) (e^s – e^a) (4.19)

U² = su yüzeyinden 2 metre yukarıdaki rüzgar hızı, e^s = su yüzeyi sıcaklığında doymuş buhar basıncı ve e^a = belirli bir yükseklikteki havanın buhar basıncı.

Marciano ve Harbeck formülü, ABD (Marciano ve Harbeck, 1954)

E(cm gün_–1) = 0.0918U⁸(e^s – e⁸) (4.20)

E(cm gün)_–1 = 0.1156U⁴(e^s – e²) (4.21)

Kuzmin Formülü, SSCB (Kuzmin, 1957) – yüzey rezervuarı >20–100 metre

E(cm ay_–1) = 15.24 (1 + 0.13U^s ) (e^s – e^a) (4.22)

United States Geological Survey (USGS), ABD ve Bureau of Reclamation formülü (USGS, 1977)

E(cm/yıl_–1) = 4.57T + 43.3 (4.23)

T = °C olarak ortalama yıllık sıcaklık

Shahtin Mamboub formülü, Mısır (Mutreja, 1986)

E(cm gün–1) = 0.35(es – ea) (1 – 0.15U2) (4.24)

es = su seviyesi sıcaklığında doymuş buhar basıncı (cm Hg–1) ve ea = Aktüel buhar basıncı (cm Hg–1)

Yukarıdaki eşitlişlerde tanımlanmazsa, rüzgar hızı (U) km x saat–1 ve buhar basıncı cm olarak civa yüksekliğidir. İlaveten ölçümlerde metre olarak alınan yüksekliğe tekabül eden terimlere ilşikin indisler alınmaktadır. Ayrıca, buhar basıncı terimi (e) ölçüm aralığı boyunca ortalama hava sıcaklığındaki doymuş buhar basıncı olarak alınır.

Eşitlikler ölçmesi çok zor olan su kütlesi yüzey sıcaklığına ihtiyaç duyar. Eğer bu ortalama hav sıcaklığı ile yer değiştirilirse o zaman buharlaşmadaki göl adveksiyon enerjisinin etkileri göz önüne alınmaz. Bu hesaplamalarda büyük hatalara sebep olan sıcaklıktaki küçük hatalar gibi buharlaşma miktarının hesaplanmasında oluşan olukça büyük hatayı ortaya çıkarır. Bundan fazla rüzgar hızı ve buhar basıncı ölçümleri kullanılan eşitlikte belirtilen yükseklikte yapılır. Genellikle değişik yüksekliklerde toplanan veriyi uyarlamak zordur çünkü doğru bir rüzgar kanunu veya yükseklikle nemin değişimini tanımlayan kanun henüz mevcut değildir.

Bu empirik formülün kullanımındaki en büyük sebep, mevcut standart meteorolojik veriyle kullanılmasının basitliğinde yatar. Bütün bunlara rağmen empirik formülün kısıtlamaları açıkca anlaşılmalıdır.