Ana Sayfa › Meteorolojik Bilgiler › e-Kütüphane
İklim bilinen değişkenliği ve şiddeti sel ve kuraklığın sıklığı üzerindeki beklenen etkisi göz önüne alındığında, tahminin önemini son yıllarda dahada artırmıştır. Bu bölümde herhangi bir tahmin sisteminin bileşenlerinin parçalarını oluşturan temel matematiksel ve hidrolojik teknikler açıklanmaktadır. Yöntemlerin seçimi ve parametrelerin ölçütlerinin belirlenmesi kısa tartışma çerçevesinde sağlanır. Belirli uygulamalar için bu bileşenlerin kullanımı örnekleri kısım-7.6-7.4’de verilmiştir.
Taşkın tahmin işlemini yapmak, zaman ve tahminin doğruluk derecesi çevresinde mevcuttur. Aslında, profesyonel bir tahmin yapmak belirlenen zamana karşı yarış gerektiriyor. Açıkça, kuruluşlar tarafından kullnılan tahmin modellerinin güvenilir, basit ve uyarı için yeterli zaman sağlayan ve istenen bir doğruluk derecesini sağlama yeteneğine sahip olması gerekir. Model seçimi aşağıdaki faktörlere bağlıdır bunlar: kullanılabilir veri miktarı; hidrolojik işlemlerin karmaşıklığı model olarak; güvenilirlik, gerekli doğruluk ve sonuçlanma süresi; türü ve selin meydana gelme sıklığı ile kullanıcı ihtiyaçları.
Çok detaylı fonksiyonları içeren kapsamlı bir modele çok ayrıntılı veri girişi gereksinimleri olabilir bu durum uyarı zamanı ve doğruluk derecesinde büyük ölçüde bir artışa neden olabilir. Bir model için bütün girdi verileri gerçek zamanlı olarak mevcut olmayabilir. Bu nedenle, pratik bir noktadan bakışla, bir taşkın tahmin modeli aşağıdaki kriterleri sağlamalıdır.
(a) Yeterli uyarı zamanıyla güvenilir tahminler sağlaması;
(b) Makul bir doğruluk derecesine sahip;
(c) Ekdeki kullanılabilir veri ve mali imkanlar dahilinde, hem kalibrasyonu için ve hemde operasyonel kullanım için veri gereksinimlerini karşılamak;
(d) Kolay anlaşılabilir fonksiyon özellikleri;
(e) Orta eğitimli operasyonel personeli tarafından işletilecek oranda basit olması.
Nitekim seçim asla belirli bir modele sınırlı olmalıdır. Her zaman farklı koşullardaki modellerin uygunluğu hakkında detayları belirlemek için seçilmiş her modelin mümkün olduğunca çok sayıda modelle kalibre edilmesi arzu edilir. Bu modellerin altında çalıştırılmış oldukları koşullara göre uygulanması gerekir.
Oldukça karmaşık olan kapsamlı modeller genellikle bilişim imkanları bakımından uygun boyuttaki bilgisayarlar olanakları gerektirir. Ancak, çoğu yerlerde bu türden tesisler mevcut değildir. Bazen uygun eğitilmiş personel bulunamaz; üstelik bu sistemlerin elektrik arızaları gibi yinelenen sorunları nedeniyle faaliyetlerinin devamı sağlanamaz. Bu nedenle, bilgisayar tabanlı kapsamlı modeller geliştirilirken hemde modellerin basit tipleri geliştirilebilmiştir. Bilgisayar tabanlı teknik genel olarak kullanılabilir ve acil durumlarda, genellikle basit bir türü olan geleneksel teknikleri benimsemiştir.
Farklı modelleri seçimi dışında farklı koşullar altında modellerin bir kalibrasyon işlemine tabi tutulması tercih edilir. Örneğin, bir model uygun genişlikteki bir ağın verileriyle kalibre edilebilir, ancak aynı zamanda bu modeli daha küçük boyuttaki bir veri ağı içinde de kalibre edilmesi gerekir ve bu gözlemler ile bazı verilerin gerçek zamanlı iletilmiş olması nedeniyle oluşacak hataların göz ardı edilmemesi gerekir. Bu bile, tüm istasyonların verilerinin kullanılamayacak olduğu acil durumlarda hangi verilerin kullanılarak modelin çalıştırılması gerektiği konusunda yardımcı olacaktır. Bu durum farklı farklı koşullar altında benimsenen parametre kümesinin oluşturulmasını gerektirir.
Bir tahmin modeli geliştirmek için kullanılan analitik yaklaşım temel alınarak taşkın tahmin yöntemleri aşağıdaki gibi sınıflandırılabilir:
(a) Yöntemler, istatistiksel bir yaklaşıma dayanmaktadır;
(b) Yöntemler, bir sel oluşumu ve yayılması mekanizmasına dayalıdır.
Tarihsel verileriden istatistiksel analiz yardımıyla üretilen matematiksel ilişkiler şeklindeki yardımıyla üretilen tahmin yöntemleri geçmişte yaygın olarak kullanılmıştır. Bunların göstergeden göstergeye basit ilişkileri mevcuttur, bazı ek parametreler ve yoğun yağış dönemindeki ölçümden ölçüme ilişkilerini içerir. Bu ilişkiler kolayca geliştirilebilir ve bir sel-taşkın tahmin sistemi kurulurken yaygın bir şekilde bir başlangıç noktası olarak kullanılır. Son zamanlarda sel-taşkın tahminlerini yapmak için popülerlik kazanmış başka bir modelleme yaklaşımı Yapay Sinir Ağları’nın kullanımıdır.
Giderek, tahmin prosedürleri temel hidrolojik ve hidrolik işlemlerin tamamı daha fazla fiziksel açıklamalara dayanmaktadır. Birçok durumda, nehir boyunca akış ve aşama durumları gerektiğinde hidroloklar nehir yönlendirme modelleri ile yağış-akış modellerini birleştirilerek kullanır. Yağış kar şeklinde ise kar erimesi modelleri uygulanmaktadır. Bu modeller doğruluğu ve karmaşıklığı, bir önceki basit endeks modelleriyle çoklu-parametre kavramsal yada süreç modelleri arasında değişir. Bilgisayar ve telemetri sistemlerindeki gelişmelerin ilerlemesiyle birlikte tahmin modelleri şu anda daha fazla bilgi sağlama ve yeni verilerin gerçek zamanlı olarak dahil edilebilmesine imkan sağlayacak şekilde daha esnek durumdadırlar.
Modellerin, bu temel kategorilerde birçok çeşitleri vardır ve ençok farklıklar hidrolojik işlemlere göre değişiklik gösterir. Modeller basit olanlardan istatistiksel bir yağış-akış ilişkisinin diğer karmaşıklığı çok daha yüksek bir derece ile karakterize edilen bir yönlendirme denklemi ile birlikte de yer olabilir.
Hidrolojik modeller toplu olarak sınıflandırılabilir yarı-dağıtılmış veya dağıtılmıştır. Modeller ya olaylara güdümlüdür veya sürekli çalışır durumdudırlar. Bir modeli yalnızca belirli bir hadisenin tahmin yapmak özelliğinde bulunuyorsa, örneğin bir fırtınadan kaynaklanan yoğun sel bu gibi hadiselere güdümlü olarak bilinir. Sürekli çalışan bir model belirtilen tam bir zaman aralığında sel hidrograf tahmini yeteneğine sahiptir. Model seçimi gereksinimleri konusundaki faktörler şunlardır:
(a) Tahmin hedefleri ve gereksinimleri;
(b) Gerekli doğruluk derecesi;
(c) Veri kullanılabilirliği;
(d) İşletmedeki tesisleri kullanılabilirlik;
(e) Modelin operasyonel kullanımı ve geliştirilmesi için eğitimli personel mevcudiyeti;
(f) Modelinin güncellenme yeteneği.
Üzerinden geçen son yirmi yılda bilim deki gelişmeler bu modellerin performansında önemli ölçüde iyileştirmeler yapmıştır. Ancak, performans genellikle havza özelliklerinin tipine göre modellenmiş olmaya göre değişmektedir, verilerin kullanılabilirliği ve modelleme anlayışı operasyonel hidrolojistlerin deneyimine göre değişir. Taşkın tahmini olarak kullanılabilecek kamuya ait ve özel çok sayıda modeller bulunmaktadır. Bu Kılavuzu'nun Bölüm-6’da şu anda kullanılabilir olan hidrolojik modellerin geniş bir yelpazede değerlendirmeleri mevcuttur.
Korelasyon katsayısı iki değişken arasındaki doğrusal ilişkiyi ölçer ve bir birçok hidrolojik analizlerin temelinde yaygın olarak kullanılan matematiksel bir araçtır. Regresyon, korelasyon kavramının bir uzantısıdır bu bir değişken düzey için ilgili formülü sağlar, örneğin, mevsimlik düşük akış, birinden veya maksimum kış yeraltı suyu seviyesi gibi şu anda kullanılabilir daha fazla gözlemler konusunda (Draper ve Smith, 1966 ) bakın.
Korelasyon katsayısı hesaplamak için formül r ve n çiftleri arasındaki x ve y katsayı değerleri aşağıdaki gibidir:
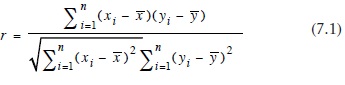
Nerede
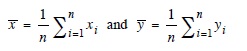
Korelasyonun olmaması ilişki olmaması anlamına gelmez R yalnızca doğrusal ilişkiyi ölçer ve örneğin, sıkı bir eğrisel ilişki mutlaka r yüksek bir değer yansıtılması değildir. Diğer taraftan, tersine iki değişken arasındaki korelasyon nedensel olarak bağlı oldukları anlamına gelmez. Grafiksel bir ilişki için ilgili meblağlar iki değişken arasındaki basit bir dağılım şeması ve sırt düzeyinde tahmin tekniği temeline dayanır (tahminlerin doğrulanması 7.3.4 bakın).
Eğer x veya y ikisinden birinin zaman serisi yapısı varsa, özellikle bir eğilim, adımlar bağlantılı olarak önce bu yapıyı kaldırmak ve önemini yorumlama konusunda dikkat edilmelidir. Ne zaman nehir deşarjı gibi bir değişkenin önceki değerleri gelecekteki bir zamanda aynı değişkenin değerini tahmin edebilmek için uygulanabilir zaman serisi teknikleri kullanılır (7.5.3 bakın).
Benzer şekilde, regresyon denklemlerinin hidroloji içinde birçok uygulamaları vardır. Genel biçimi aşağıdaki gibidir:
Y = bo + b1X1 + b2X2 + b3X3 + ... (7.2)
Nerede X değişkenleri varsa şu anda gözlemlenen ve Y değişkeni gelecekteki bir değerin tahminidir. Gözlenen Y ve X değerleri tahmini regresyon katsayıları b tarafından belirtilir. X değişkenleri akıntıya karşı katman veya akıntı, yağmur, havza koşulları, sıcaklık veya mevsimlik yağışı içerebilir. Y değişken maksimum veya minimum katmana başvurabilir. Çoklu korelasyon katsayısı açıklama ilişki derecesini ölçer. Uyumda bir başka önlem, tahmin ve standart hata başka bir kalibrasyon ölçüm kümesindeki regresyon satırından gidişin standart sapmasını ölçer. Teori tüm genel istatistiksel metinler de açıklanmıştır.
Değişkenlerin doğrusal kombinasyonları bazen yetersiz ve bu ya X veya Y normalleştirmek için gereklidir. Güçlü dönüşüm yöntemi tarafından aşağıdaki eşitlikler vasıtasıyla YT Y dönüştürmek için kullanılabilir:
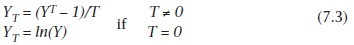
Güç, sürekli T ölçekte logaritmik ve harmonik dönüşümleri kapsar. Deneme ve yanılma yöntemiyle çarpıklık azaltan veya grafik olarak kullanarak şekil II.7.4 deki diyagramlar gibi uygun bir T değeri bulunabilir.
Doğrusal olmayan polinomları da kullanarak bir regresyon Örneğin, Xi, Xi2 veya Xi 3 kullanarak sağlanabilir. Alternatif olarak, fonksiyon-minimizasyon rutinlerini kullanılarak doğrusal olmayan regresyon güçlü doğrusal olmayan denklemlerin uygun parametreleri basitçe uygulanan bir rota sunuyor. Önemli ölçüde açıklayıcı değişkenler kümesi karar için yararlı çok büyük potansiyel kümesinden bir alt küme seçimi ve özelliklede, kalıntılar arasındaki farkların dikkatli incelemesine, kalibrasyon veri kümesi içinde gözlenen ve tahmin edilen değerler arsındaki farklıklara bakmak gerekir. Büyük ölçüdeki kalıntılara yol açan koşullar sık sık yapılması gereken ayarlamaları göstergesidir. Avantaj bilgisayar olanakları ve bir dizi alternatif kombinasyonları keşfetmek için artıkların grafik görüntüleri alınmalıdır. Tamamen otomatik arama ve seçim yöntemlerinin özel kullanımıyla olduğu gibi, adım adım, anlamlı evre, geriye ve ileriye doğru seçim ve en iyi alt kümelerinden kaçınılmalıdır.
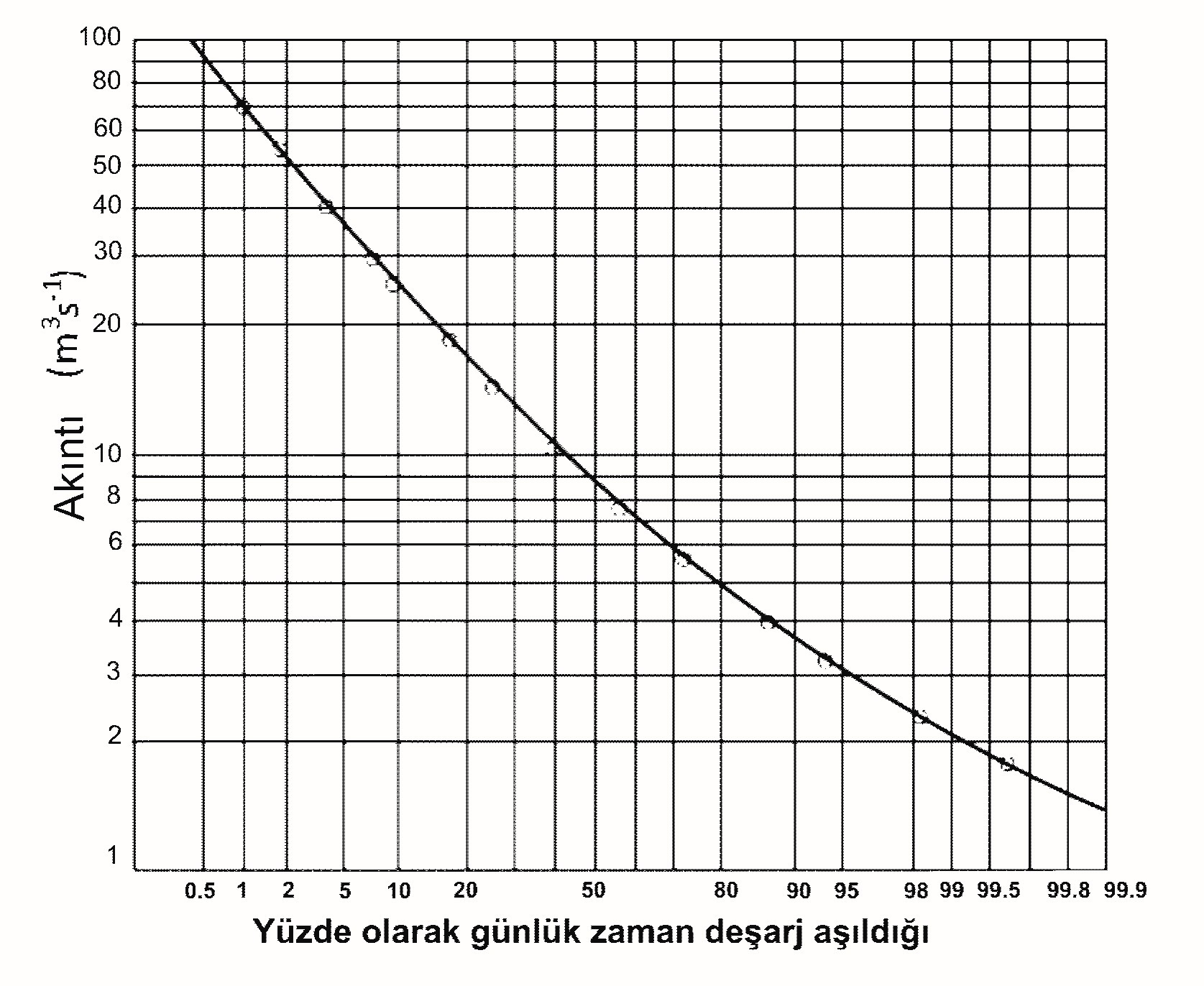
Şekil 4. Günlük debi-akış zaman eğrisi
Tahminlerde sorunlar için regresyon uygulama örnekleri 7.3.2.3 ve 7.4.7. ‘de verilmiştir.
Geçmiş yağış indeksi 6.3.2.2 açıklanmıştır. Bu yöntem birçok ülkede operasyonel tahmin için bir temel araç olmuştur. Tahmin zamanında önceden meydana gelen yağış etkisini ölçmek olarak, toprağın üst düzeyinde nem oluşturduğundan bir dizin sağlar. En sık karşılaşılan indeks önceden oluşan yağış indeksi ve önceden oluşmuş nem dizini koşulunun mevcudiyetidir. Nem dizisi indeksleme yöntemleri hidrolojik tahmin için uygulamalarına göre iki ana özelliklere sahiptir. İlk olarak, dizin günlük olarak güncelleştirildiğinden, sürekli modelleme yerine analiz için bir olay türünün seçimi uygundur. Böylece, çoğu tahmin için bu yöntemi uygulayabilmek amacıyla bu olayların bir yağış dönemine bölmek veya bir olayı ayrı yağış dönemlerine bölmek gereklidir. Örneğin, az yağış olduğu veya yağış hiç olmadığı, kısa süreli kesintiyle oluşan yağışın uzun süre kullanılmadığı zamanlarda, bir veya birkaç oluşan fırtınaların dahil olup olmadığına dair karar vermek zor olabilir.
İkinci özelliği, hesaplanan yüzey akış hacmi bir birim hidrograf uygulandığında sadece hidrograftan üretilen birim yüzey akışıdır. Toplam akış hidrografını sentezlemek için temel akış tarafından başka bir yöntemi ile belirlenmesi gerekir. Teknik olay akış ve önemi yalnızca basit bir yaklaşım olduğunu kabul edilebilir tüm operasyonel kullanımı gereksizdir. Operasyonel kullanımın konusunda yalnızca akış olayının önemi ve tüm kabul edilebilir basit bir yaklaşım tekniği vardır.
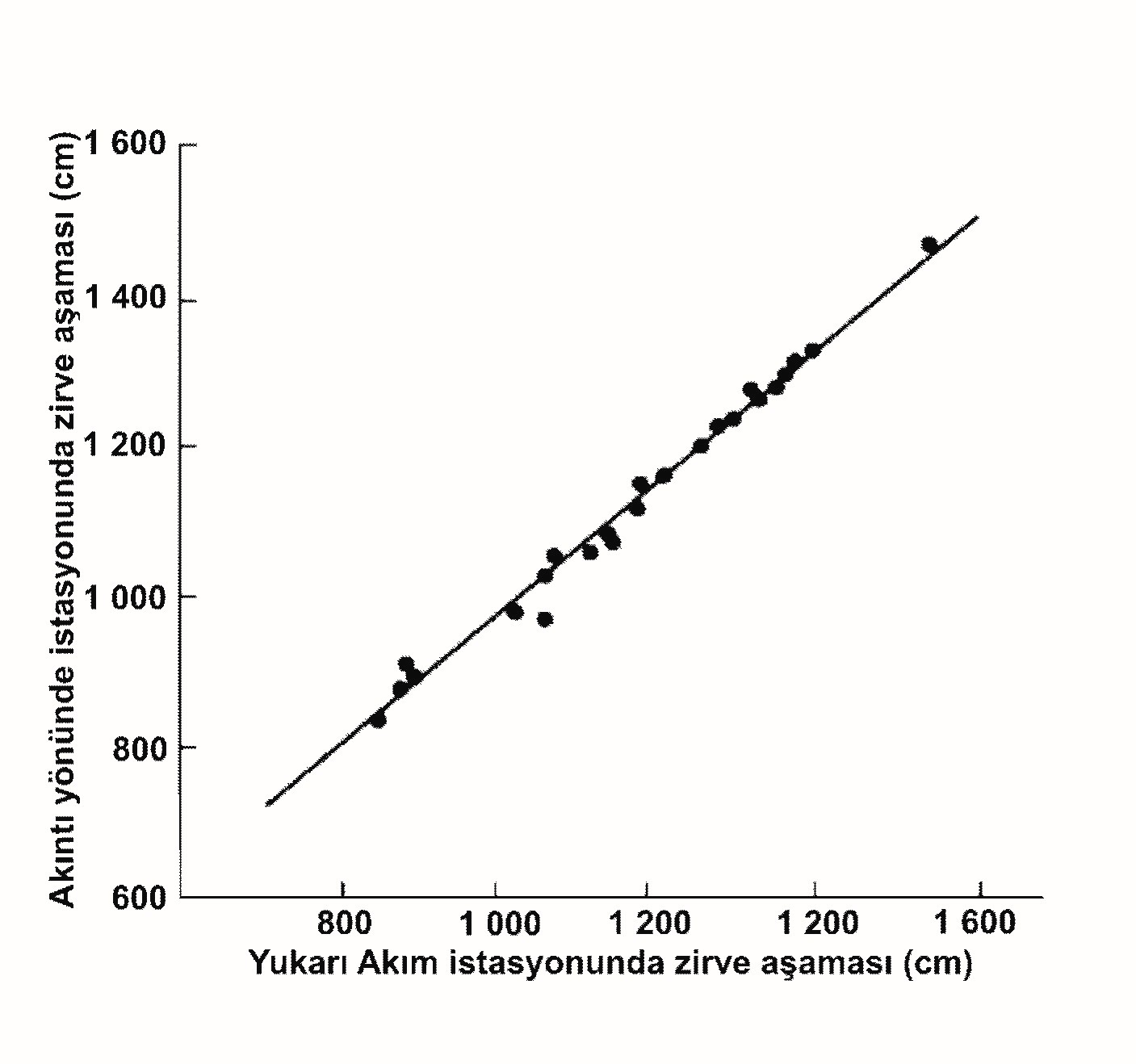
Çok yaygın bir olay için, en büyük aşamayı veya zirveyi tahmin etmek zorunludur. Orta ölçekli nehirler ile ilgili olarak kullanılan kanıtlanmış bir pratik yöntem bir akıntıya sahne olan hidrografta, böylece bir sürüklenme zamanı taşkın dalgasının hareket süresi eşit olan bir tahmin sağlayan basit bir grafik ilişkisi oluşturma tekniğidir. Şekil II.7.5 bu presedürü göstermektedir.
Akıntıya karşı tahmin çıktısı için akım yönünde bir girdi sağlar, böylece zincir gibi tepeden tepeye tahminler yaygındır. Bu tür grafiklerde genellikle hesaplamalar yükseliş ve düşüş dönemlerindeki gecikme süresi içinde farklar alınırsa hidrografları tahmin etmek için kullanılabilir. Aşağıdaki korelasyon ilişkisi basittir, istasyonlar arasındaki ilişkilerin (Şekil II.7.5) başarılı olduğu durumlarda yararlıdır:

Burada h1 ve h2 bir akışın bir üst ve bir alt akım istasyonunda maksimum aşamalarını göstermektedir, sırasıyla, Iloc istasyonları arasında yerel girişlerin olması ve Δt gecikme zamanıdır. Şekil II.7.6 Bu tür ilişkinin bir örneği verilir. Uygun zamanlarda iki veya daha fazla yukarı akım istasyonlarında deşarjların toplamları kombine bir değişken yerine bireysel akarsu kolu aşama yüksekliği gibi, korelasyon değişkenlerin sayısını azaltabilir. Bu temel yaklaşımlar üzerine çeşitlemeler seyahat süresi ve kolun girişinin farklı şartlara göre tasarlanmış olabilir. Grafiksel yaklaşım çoklu regresyon (7.3.2.1 bakın) yararlanarak tamamen sayısal biri tarafından değiştirilebilir. Regresyon denklemi aşağıdaki formu alabilir:
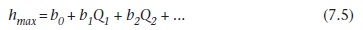
Burada Q1Q2 ... akıntıya belirli bir anda istasyonlarda deşarjları vardır. Diğer açıklayıcı değişkenleri, yağış ve öncül havza koşulları gibi (7.3.2.2) bu tür veya ilave deşarj için yerine getirilecektir.
Modellerin pek çok temel kategorisi vardır ve bu çoğu hidrolojik süreçlerin nasıl kavramsallaştırıldığına göre değişir. Hidrolojik modeller ve/veya tahmin işlemleri gerçek zamanlı yağış ve akarsu akış verileri kullanmak ve gelecekteki akışı koşulları gözlenen koşullara göre değişmektedir.

Şekil 4. Volga nehir için tepe etap ve seyahat süresi
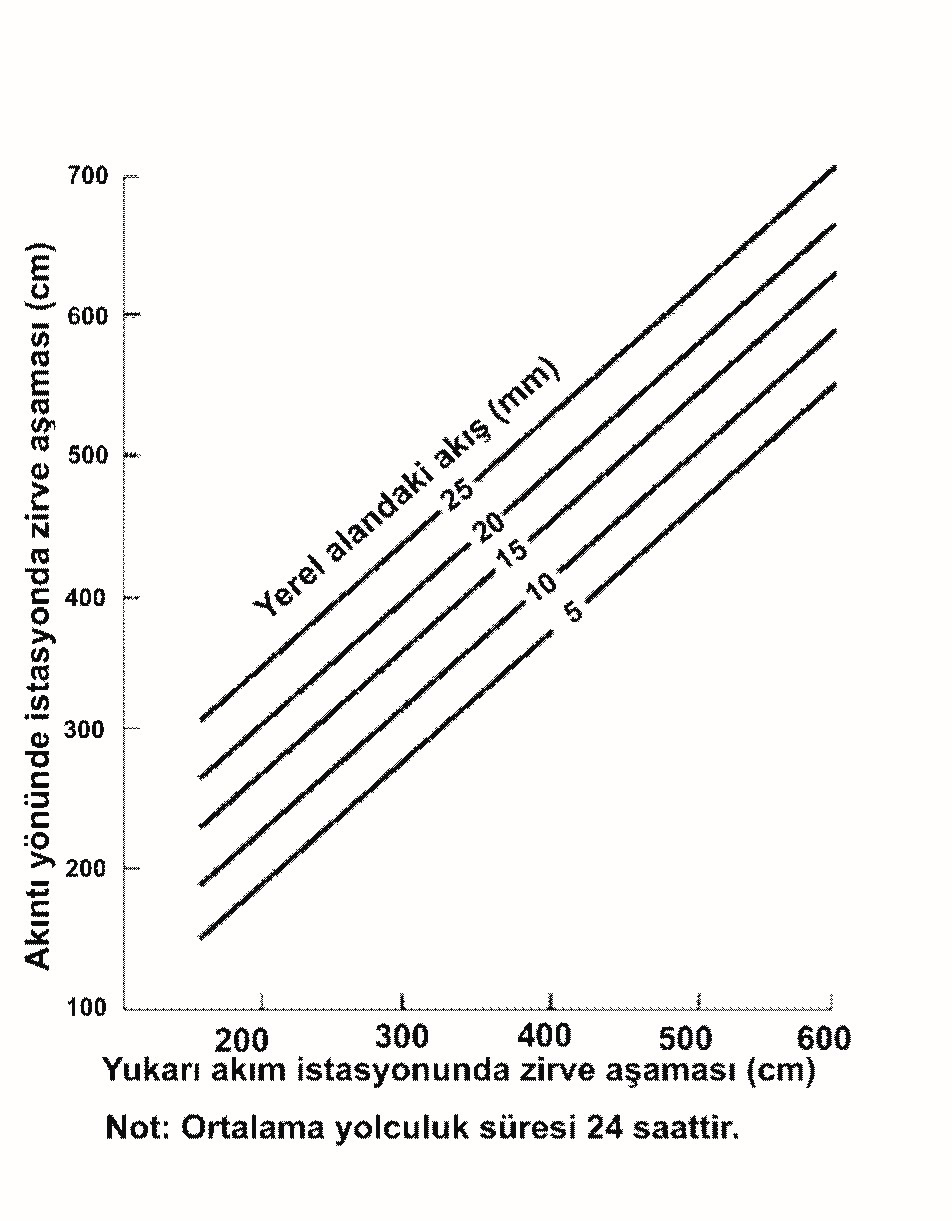
Şekil 5. Yerel akış için değişkenler ile tipik gösterge ilişki
Hidrolojik modeller veya prosedürlerin karmaşıklığı, doğruluk ve kullanım kolaylığına göre değişir. Basit hidrolojik modeller tablolar, grafikler ya da deneysel olarak elde edilen ilişkilerden oluşmaktadır. Daha karmaşık hidrolojik modelleme sistemleri yerinde kullanımı ve uzaktan algılama verisi ve çoklu hidrolojik modeller çok doğru hidrolojik tahmin üretmek için entegre edilmiştir. Kişisel bilgisayar teknolojisinde yeni gelişmeler göre bu tür bilgisayarlarda çalışabilecek mümkün olduğunca armaşık modelleme sistemlerinin çalıştırılmasını mümkün kılmıştır. Bu sistemleri kullanın ve idamesi kendinden öncekilerden daha kolaydır.
Üzerinden bilim ve performans modellerin iyileştirilmesinde geçmiş yirmi yılda büyük atılımlar yapılmıştır. Model performansı modelin türüne, veri kullanılabilirliğine, modellerin kalibre edilebilmesi ve modeli uygulayacak olan hidrolojistin deneyimi ile model mekanik anlayışına ve modellenecek havza özelliklerinin tipine göre değişir. Veri genellikle operasyonel uygulamada kabul edilebilir doğruluğa ulaşmada sınırlayıcı etkendir. Ancak, GIS veri kullanılabilirliğinde gelişmesiyle birlikte, hidrolojik modelleri sadece tarihsel hidrolojik veriler dayanak olmadan da kalibre edebilmek için model parametreleri tahmin edilebilir.
Meteoroloji radarlarının yüksek mekansal ve zamansal çözünürlüğü ile operasyonel yağış tahminleri kullanılabilirliğini ve bilgisayar gücündeki önemli gelişmeler dağıtılmış hidrolojik modellerin kullanımını mümkün kılmıştır. Dağıtılmış modellerde toprak yüzeyi ve toprak özelliklerinin dağıtılmış veritabanları gelişimi nedeniyle bir zenginlik vardır. (Carpenter ve diğerleri (2001), Ogden ve diğerleri (2001), Beven (2002), Smith ve diğerleri (2004a)) dağıtılmış hidrolojik modelleme, son genel bakışlar ve operasyonel tahmin için olası kullanımı çevreleyen sorunları sağlar.
Yağış gidişatındaki belirsizliklerin önemli etkisi ve model yapısı ve ani sel oluşumu küçük ölçeklerde parametre hataları operasyonel tahminler için dağıtılmış modellerin erken kullanımı engellemiştir. Bununla birlikte, dağıtılmış modeller ek bilgi sağlamak için ve mevcut akarsu akışı gözlem olmadığı yerlerde hidrolojik koşullar ile ilgili bilgileri temin etmek. Amerika Birleşik Devletleri'nde, NOAA sponsorluğundaki dağıtılmış modeli Intercom Parison Projesi operasyonel kalite verileri kullanarak Dağıtılmış modelleri uygulanabilirliğini araştırmak ve bunların kullanımları ile çevreleyen sorunlarını vurgulamak için bir forum oluşturulmuştur (Smith ve diğerleri, 2004b). Küçük ölçekli yağış tahminlerindeki belirsizlik (bakınız, 2000 collier ve Krzysztofowicz ) ve hidrolojik model hatalarının hesabı için dağıtılmış hidrolojik modeller kullanılarak ani-sel-eğilimli alanlarda hesaplama yapma yöntemi yerine olasılık üretmek yöntemlerinin kulalnımı tavsiye edilir. Bu alan için olasılıksal akış tahmini öngörülmesiyle etkin hidrolojik araştırma alanı olmaya devam etmektedir (bakınız, Carpenter ve Georgakakos, 2004).
Tahmin durumu ayarlamaları genellikle model çıktı ve değişkenleri doğrudan ölçümlerine dayanmaktadır. Tahminlerini güncelleştirmesi için birçok teknikler vardır. Eğer Yi tahmin çıktınsın bir gözlemi yapılmıiş ise, bilinen tahmin hatasını yararları ile bir sonraki tahminleri ayarlamak için bir fırsat oluşturmaktadır 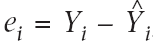 , burada
, burada 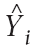 tahminin tahminidir. Çoğu ayarlamalar tahmincinin öznel yargısının sonucudur, ancak çeşitli matematiksel tekniklerin biçimlendirilmiş olması bu işlem sürecine izin verir. Resmi yaklaşımın temel prensipleri aşağıda açıklanmıştır.
tahminin tahminidir. Çoğu ayarlamalar tahmincinin öznel yargısının sonucudur, ancak çeşitli matematiksel tekniklerin biçimlendirilmiş olması bu işlem sürecine izin verir. Resmi yaklaşımın temel prensipleri aşağıda açıklanmıştır.
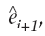 periyodiksel yeni hata e tahmin etmek için yürütülmüş olabilir, potansiyel yeni hata tahminleri ayıklamak için bir zaman serisi analizi için yeni tahminlerini
periyodiksel yeni hata e tahmin etmek için yürütülmüş olabilir, potansiyel yeni hata tahminleri ayıklamak için bir zaman serisi analizi için yeni tahminlerini 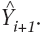 değiştirmek için kullanılabilir. Gerçek zamanlı model güncelleştirmesinin iki ana türü vardır:
değiştirmek için kullanılabilir. Gerçek zamanlı model güncelleştirmesinin iki ana türü vardır:
(a) Parametre güncelleştirme, burada büyük olasılıkla tüm veya bazı model parametrelerinin tahminleri yağış ve akış gibi gelen verileri temel alınarak düzenli olarak güncelleştirilir. Bu verileri aynı zamanda geleneksel telemetri veya daha modern kontrollü gözetim ve kısaltma olarak bilinen SCADA veri edinme sistemlerinden elde edilir;
(b) Durumu güncelleştirme, burada akım veya su seviyesi gibi modeldeki durum değişkenlerinin tahminleri gelen temel verileri dikkate alınarak düzenli olarak güncelleştirilir.
Bazen bu güncelleştirme işlemleri genişletilmiş Kalman filtresi gibi bazı parametre durumu tahmini algoritması formu kullanılarak tam bütünleşmiş bir şekilde gerçekleştirilir. Alternatif olarak, onlar aynı anda ama ayrı algoritmalarla yapılmaktadır. Alınabilen yeni tahminler önceki tahminleri işlevlerini artı tahmini hata işlevi olan bir tekrarlamalı şekilde verileri işlemek için bu algoritmaları normalde tekrarlamalı tahmin algoritmaları olarak bilinir. Bu algoritma örnekleri özyinelemeli en küçük kareler algoritmalarıdır, operasyonel hidroloji yaygın olarak kullanılan algoritmalar (Cluckie ve Han, 2000 bakın) ve tekrarlamalı aracı değişkenler algoritması olarak Young (1993) açıklanmıştır.
Kalman filtresi ve genişletilmiş Kalman filtresi hidrolojik tahmin için uygulanan tekrarlamalı tahmin teknikleri, ancak tahmin modelinin analizi için uygun biçimde olmasını sağlamak için önemli matematiksel ve hidrolojik becerileri gerektirir.
Genel biçimli tekrarlanan parametre tahmini algoritması aşağıdaki gibidir: Genel biçim durumu tahmini algoritması ise:
Yenilikler süreci (tek-adım ileriye tahmini üretimi)
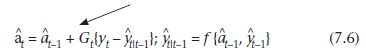
Genel form durumu tahmini algoritması ise:
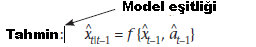
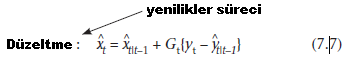
Burada y = g {xt} bazı tanımlanan şekilde modelinin durum değişkenlerine bağlı olduğu gözlenen veri ve Gt ise genellikle ayrıca hesaplanan yinelemeli ve parametre veya durumu tahminlerinde belirsizlik işlevi sistem kazanç olarak adlandırılan bir zaman değişken matristir. Bu iki tekrarlamalı tahmini işlemlerini birleştiren bir algoritmaya genellikle bir veri asimilasyon algoritması denir (bakın genç, 1993).
Ancak, hidrolojik model çıktı ayarlamak için daha kavramsal bir tekniği de kullanılabilir. Yöntem model yapısı veya modelinde kullanılan algoritmaları herhangi bir değişiklik gerektirmez. Bunun yerine, bu yaklaşım giriş verisi ve sonuç olarak daha yakından geçerli ve önceki akışlarını yeniden oluşturmak şekilde durum değişkenlerini ayarlar. Bu düzeltilmiş değerleri sonra hidrograf tahmin etmek için kullanılır.
Tahmin ayarlamaların yalnızca modelin çıktı temeline dayalı olması gerekmez. Bu da model tarafından oluşturulmuş değerler ile karşılaştırma için durum değişkenlerinin ölçümleri yapılarak gerçekleştirilmesiyle başarılı olur. Örneğin, böyle bir teknikle gözlenen kar örtüsü su eşdeğeri ölçümleri kavramsal modelinden türetilen mevsimlik su tedarik tahminleri geliştirme aracı olarak kullanır. Pratikte, fiziksel kimliklerini kaybetmesi gibi durumu değişkenleri modeli basitleştirmeleri sağladığından, modelin durum değişkenlerinin alan ölçülerini sayısal olarak oluşturulan değerleri doğrudan ikame etmesi yanlış olacaktır.
Tahmin doğrulama bir dizi şeklinde tahminler ile buna karşılık gelen bir gözlem dizisi arasındaki ilişkiyi karakterize etmektedir. Tahmin sistemleri idari, bilimsel ve kullanıcı odaklı doğrulama prosödürlerinden geçmemiş ise bu tahmin sistemi tahmine bağlı eylem için tamamlanmış sayılmayacaktır.
İstatistikleri çeşitli tahmin becerilerini değerlendirmek amacıyla hesaplanır. Kullanılacak istatistik yöntemi tahminin türü ve tahminin doğrulama amacına bağlıdır. Bir çalışma, etkili bir şekilde tahmin becerilerini ayırdetmek için önerilen ölçümler çerçevesinde yardımcı bir doğrulama programı, yürütülen çalışmadan önce yapılmalıdır.
Bir doğrulama sistemini etkili olması için tahminlerin arşivi ve buna karşı tahminleri kıyaslayabilecek olan gözlem verilerini içermelidir. Ayrıca, hesaplanan temel bir tahmin doğrulama tedbirleri desteklemesi bakımından yorumlarıyla birlikte dahil edilmelidir. Temel tahmin sisteminin seçimi, doğrulanacak tahmin türü ve tahminlerini geliştirmek için kullanılan tahmin süreçlerine bağlı olmaktadır. İki günden daha az olan kısa vadeli deterministik tahminleri için kararlılık yararlı bir dayanak olmaktadır.
Uzun vadeli tahminler ve olasılık tahminleri için, klimatoloji dağıtımları veya gecikmeli iklimbilimi için daha uygun dayanaklar mevcuttur. Tahmin süreci birkaç adımdan oluşur, her adımda tahmin işlemi doğrulamayı etkinleştirmek için ek ara verilerininde arşivlenmiş olması gerekir. Mümkünse, tahminlerde heasaplamak amacıyla kullanılan tahmin sürecinin güncelleştirmesi hindcast (tahmin yöntemi) çalışmalarını etkinleştirmek için kullanılan giriş verilerinin arşivlenmesi gerekmektedir. Veri derecelendirme eğrileri dahil olmak üzere, yağış ve sıcaklık ile model parametreleri gibi gözlemler, giriş tahmin girdilerini içeren verilerde arşivlenmelidir. Joliffe ve Stephenson (2003) daha ayrıntılı bilgi sağlayan mükemmel bir referans mevcuttur. 1995 yılında, WMO Taşkın tahmin sistemleri yönetimine genel bakış sağlamak için MOFFS’u geliştirilmiş, burada taşkın tahmini konunda hızı sağlayan bir uluslararası ilgili temel arama sistemleri, taşkınlarda nehirler için belirtilen tetikleyici seviyelerinin aşılma durumuna dayalı taşkın tahmin sistemlerinin performansı hakkında bilgi odaklı yönetim bakışı geliştirdi. MOFFS amacı, tesislerdeki eksiklikleri vurgulamak ve sonraki sel olayı oluşmadan önce hataları düzeltmek için uygun yönetim eylem planlarıyla alınabilir tedbirleri sağlamak ve bireysel taşkın tahmin sistemlerinin performans eksikliklerinin neler olduğunu hızla belirlemek ve vurgulamaktır.