Ana Sayfa › Genel › e-Kütüphane
İçindekiler
Alandaki bir noktada hidrolojik değişkenin gözlemsel zaman serisi birçok hidrolojik verileri içerir. Hidrolojik verilerin tek bir zaman serisi incelenmesi uzayda bir noktada bu değişkenin zamansal ilişki yapısının belirlenmesini sağlar. Birden fazla değişken istasyonundan gözlemler karşılanabiliyorsa, aynı mekansal noktanın çok değişkenli zaman serileri arasındaki ilişki çapraz korelasyonlar yapılarak incelenebilir. Alanda belli bazı noktalar aynı değişkenin zaman serisi göz önüne alarak, bu hidrolojik bir değişkenin bir mekansal-zamansal alan ve keşfedilmeyi farklı mekansal noktalarda aynı değişkenin zaman serisi arasındaki bir çapraz korelasyonla incelenebilmektedir. Bu geçici bir yorumlama mümkündür ve/veya hidrolojik süreçlerin ve buradan sentetik bir akarsu akışı oluşturma ve genişletme gibi veri ve bilinenlere dayanan tahmin boşluklarını doldurmak için kullanılacak zamansal kayma yapısı sağlar.
Düzenli veya düzensiz aralıklarla kesikli zaman anlarındaki örneklerinde olduğu için ya da nicemlenerek zaman serisinin her bir değeri üzerinden bir değişkeni ayrılmaz ise hidrolojik zaman serisinin ve sürekli olarak kayıt cihazından türetilmiştir, ayrık ve kesintisiz yapılabilir zaman aralığı tanımlanır. Sürekli zaman serisleri geçici veya operasyonel etki alanında belirli durumlarda kullanışlı olabilir. Örneğin, Fourier ya da Laplace ayrılmaz dönüşümler ile analiz edilebilir.
Ne zaman çalışma yapılırsa, hidrolojik bir zaman serisinin uygun zaman aralıklarında kullanmak önemlidir. Veriler saatlik, günlük, aylık ya da yıllık olabilir, ancak belirli bir uygulamada veri toplama veya daha uzun bir süre ya da daha kısa bir süre gerektiren veri yükünün zorunlu zaman aralığını kullanmak gerekli olabilir. Bu serinin özellikleri üzerine etkileri vardır. Korelasyon katsayısının yıllık değerleri gelen bir dizinin korelasyonu sıfıra düşebilir iken, saatlik akım serilerinin çok yüksek korelasyon değerleri içerebilmesi muhtemeldir.
Box ve Jenkins (1970) kullanıcısı tarafından muazzam monografı dahil olmak üzere zaman serilerinin analizleri ile ilgili geniş çaplı bir literatür bulunmaktadır. Hidrolojik uygulamalar, zaman serisi analizi, Salas (1992)'de incelenebilir. Zaman serileri analizlerinin elemanları yaygın olarak genel amaçlı istatistiksel yazılım paketlerine dahil edilmiştir. Bu bölümde kısaca hidrolojik bir kayıtlardaki Olasılıksal benzetim ve değişim tespiti ile ilgili alandaki uygulamalı sorunlar açıklanır.
Stokastik modeller kara kutu modelleri olan gözlemlenmiş zaman serilerinin istatistiksel özelliklerinden tahmin edilmiş olduğu parametreleridir. Stokastik yöntemler ilk depolama rezervuarlarının tasarımı ile bağlantılı olarak hidrolojide uygulamaya konmuştur. Yıllık veya aylık akış hacimleri, ancak bu tür amaçlar için yeterli ayrıntı sağlamak için rezervuar kapasitesinin en iyi akış dizileri kümesinden değerlendirilebilecek akışının kritik bir dizilerini meydana gelme olasılığını yansıtmalıdır. Her bir süre uzun yıllık süre gerekir ve ilgili istatistiksel özellikleri açısından da şimdiye kadar onun hakkında tarihi rekor ayırt edilemez olmalıdır. Korunacak olan tarihsel kayıtların istatistiksel özellikleri uygun bir stokastik modelin seçiminde temel sorun vardır. Modelleme, çok daha fazla iç korelasyonlarla korunmuş olması şartı nedeniyle havzasında iki veya daha fazla rezervuar alanları için eş zamanlı akış dizilerini oluşturmak için gerekli olması durumunda zordur. Stokastik modelleme gerçek zamanlı akış tahminleri güven sınırları içinde kurulmasında kullanılmıştır. Bu tür uygulamalara burada daha fazla iyileştirme verilmemektedir. Tasarım ve depolama rezervuarlarının işletmesiyle ilgili bir tartışma 4.2 de sağlanmaktadır.
Aylık, mevsimsel veya yıllık akış hacimlerinin simülasyonu için birçok modelin herhangi dönemindeki akış, rastgele bir dürtü ayrıca bir önceki dönemde akım kullanıcısı tarafından belirlenmiş olduğunu varsaymaktadır, birinci dereceden Markov yapısını varsayabiliriz. Yıllık akımlar için bu tip bir model olarak ifade edilebilir:
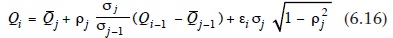
Burada Qi akışı 1 ay ya da yıl bakılmaksızın ardışık olarak numaralandırma dizisinin ith üyesi olduğu, Qj değeri Jth ay için ortalama akışıdır, j değeri ay için standart sapma, ρj değeri Qj ve Qj–1 arasındaki seri korelasyon olduğunu ve i ve P sıfır birim varyans ve seri bağımsızlık ortalaması ile uygun bir dağılımla rasgele bir değişken türetimi konumundadır.
Denklem 6.16 mevsimsel akımlar (j = 1, 2, 3, 4) ve yıllık akımlar için (j = 1) uygun olmaktadır. Sonraki durumunda bu hale gelir:
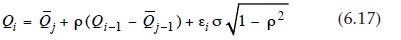
Q δve ρ, değerleri tarihsel kayıtlarından türetilmiştir ve amaçları hizmet verebilmek için uygulanabilir olduğu varsayılmaktadır, Qi-l bir başlangıç değeri sadece seçilmiş olması gereken herhangi bir uzunluktaki bir seri benzetimidir. Monte Carlo teknikleri genellikle bilgisayar tarafından türetilen rasgele değişkenlerin sıralı değerleri kullanılır. Esas itibariyle, denklemlerde 6.16 tasvir modellerinin geliştirmesi ve uygulanması nispeten kolay ve basittir. Bununla birlikte, dikkatli bir değerlendirme ve kararlar gerektiren çeşitli çalışma kapsamındaki belirli bir sorunlar için kritik olabilir:
(a) Rastgele değişkenin dağılımı nedir?
(b) Varyansı eğer mevcutsa, seri halinde korelasyonu için düzeltilebilir mi?
(c) Hesaplanan seri korelasyon değeri ne kadar doğru?
Tek değişkenli stokastik modellerin önemli bir uzantısı Box ve Jenkinsthe (Box ve Jenkins, 1970; Hipel ve diğerleri, 1977): tarafından geliştirilen özbağlanımlı hareketli ortalama modelleri (ARMA) grup tarafından temsil edilmektedir.
Üç türü vardır: özbağlanımlı hareketli ortalama (otoregresif) (AR), hareketli ortalama (MA) ve karışık (ARMA) modeller. Sırasıyla p ve q ve türü q hareketli ortalama (MA), en genel türü (ARMA), sırasıyla şunlardır:
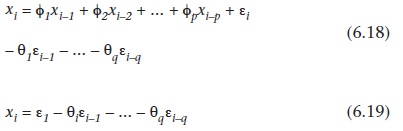
Burada Xi ortalama serisi gözlem sapması olduğunu, 1 ve 1 tahmin edilecek parametreleri ve i yukarıda tanımlanmış rastgele bir değişken olarak (6.2.2.1 bakın) temsil edilir.
Sistematik bir yaklaşım uygulaması için ARMA modelleri geliştirilmiştir (Box ve Jenkins, 1970):
(a) Tanımlama: Dizisel korelasyon tablosu serisi altında çalışma düzeni ve uygun türü seçme temelinde çeşitli ARMA modelleri otokorolasyon fonksiyonları ile karşılaştırıldığında;
(b) Tahmin: Model parametreleri, momentler yöntemi kullanılarak (Salas, 1992) tahmin edilmektedir, maksimum olabilirlik yönteminin veya kareler kalanların toplamının en aza indirerek tahminleri seçilen en küçük kareler yöntemi;
(c) Tanı kontrol: kalanlar rastgele seçilen model yeterliliği doğrulamak için kontrol edilir.
Otoregresif hareketli ortalama modelleri, daha önce açıklandığı şekilde Monte Carlo teknikleri ile sentetik akış dizileri oluşturmak için kullanılır. Bunu olasılıksal üretim yöntemlerinin dikkatle ve çalışması kapsamında su kaynakları projesi için önemli olan kaydın özelliklerinden önemli olduğu göz önünde bulundurarak kullanılması gerektiğinin akılda tutulması önemlidir.
Hurst (Hurst, 1951) keşfedilen özellikleri uzun vadeli kalıcılık veya alçak frekans elementleri barındırabilir iki adet olasılıksal modellerin geliştirilmesini sağlamıştır, içinde durağan Markov süreçleri ile oldukça uzun süre anlaşmazlık gösteren jeofiziksel yüzeyleri kaydetmektedir. Bunlardan ilki, kısmi Gauss formunda gürültü (FGN) modeli (Mandelbrot ve Wallis, 1968) oldukça düşük frekansları temsil etmekte olan Tüm Hurst olgusunu vurgulayan bir spektral yoğunluk fonksiyonu ile karakterize edilen kendine benzer, rastgele bir süreçtir. Aynı zamanda kırık çizgi sürecinin uzun bellek modelinin Tüm Hurst olgusunu koruyacağını gösterilmiştir (Rodriguez-Iturbe ve diğerleri, 1972; Mejia ve diğerleri, 1972).
Tüm Hurst bulguları mutlaka oldukça uzun vadeli kalıcılığı anlamına gelmez ve dahası, ARMA modellerin bazı versiyonları önemli düşük frekans efektleri simülasyonu yeteneğine sahiptirler. Durağan olmayan işlemin ortalama değerinin de Hurst olsun bu iklim değişikliği, insan kökenli faktörler veya sadece homojen olmayan veri serisinin uzun kayıt ve analizi sırasında bulunan özellikleri neden olabilir.
Hidrolojik veriler uzun zaman serisi değişikliklerin tespitinde önemli, bilimsel ve uygulamalı önemi olan bir konudur. Gelecekteki su kaynaklarının ve taşkın korunma planlaması için esastır. Hidrolojik sistemleri, meydana gelen değişikliler dahilinde rezervuarların, barajlar ve bentler gibi yapıların tasarlanması için varolan prosedürler dahilinde gözden geçirilerek revize edilmesi gerekir; aksi takdirde, sistemler ihtiyacın üzerinde veya altında-tasarlanmış olacaktır, bu durum bunlar ya amaca uygun yeterince hizmet vermez durumda veya gerekenden daha fazla pahalıya mal olacaktır.
Dünya İklim Programı dahilinde yürütülen faaliyetler - Su (WMO, 1988) Cavadias tarafından sunulan hidrolojik verilerin değişimi (WMO, 1992) Kundzewicz ve Robson saptanmasında kullanılan yöntem hakkında genel tavsiyeler oluşturulmasına yol açmıştır (WMO, 2000, 2004). Bu bölüm, değişiklikler için test sürecinin farklı bileşenleri ile ilgili daha detaylı tavsiyeler için başvuru olabilecek sonraki iki adet referansı esas almaktadır.
Bir zaman serisi içinde değişiklik çeşitli şekillerde ortaya çıkabilirr: yavaş yavaş ( bir eğilim), aniden (bir adımı değiştirmek) veya daha karmaşık bir biçimde. Bu ortalama, ortalama varyans, bağımlılık veya verilerle ilgili diğer konuları etkileyebilir.
Kullanıcıya istatistiksel olarak deney gerçekleştirmek amacıyla bu deney hakkında araştırma yürütmek boş ve alternatif varsayımlar tanımlamak için gereklidir. Örneğin, bir dizi ortalama eğilimi test etmek için, farksızlık hipotezi bir dizi ve anlam ya artan veya azalan zaman içinde olacaktır, alternetif hipotezlerin hiçbir değişikliği ortalamada olmadığı durumda olacaktır. Bir deney yapmak için, hipotezi doğru olduğunu varsayarak başlamak gereklidir. Sonraki adım, gözlenen verilerin bu varsayımı ile tutarlı olup olmadığını kontrol edilmesidir. Aksi takdirde, farksızlık hipotezi reddedilir.
Geçersiz ve alternatif hipotezler arasında karşılaştırmak için bir sınama istatistiği seçildiğinde ve önemi mevcut kanıtlara dayalı olarak değerlendirilir. Sınama istatistiği sadece basitçe test edilen veriler serisinden hesaplanan sayısal bir değerdir. İyi bir test istatistiğinde iki hipotez arasındaki farklılıkları vurgulamak gerekmektedir. Bir test istatistiği için basit bir örnek verirsek, ortalama bir eğilim testi için kullanılabilen doğrusal bir regresyon eğimi basit bir örnektir. Hiçbir eğilim (farksızlık hipotezi) durmunda ise, regresyon eğimi sıfıra yakın bir değere sahip olmalıdır. Büyük bir eğilim varsa (alternatif hipotez) ortalaması, regresyon eğim değeri sıfırdan çok farklı olabilir: artan bir eğilim için pozitif ve azalan bir trend için negatif olurdu.
Sınama istatistiği genellikle sıfır (farksızlık) hipotezi kapsamında oluşacak değerler aralığında önemli ölçüde farklılık olmadığını anlamlılık düzeyinde ölçer. Başkalarında mevcut olduğunda bir sınama, hatalı bir eğilimin algıladığının olasılığıdır; bu tip I hata olarak adlandırılır. Bir tip II hata sıfır (farksızlık) hipotezini kabul edilir -hiçbir eğilim mevcut değil - aslında alternatif varsayım (bir eğilim var) doğru olduğunda oluşur. Bir testin gücü doğru bir şekilde mevcut olan bir eğilimin saptanma olasılığıdır; hata II olasılığını düşük türüne sahip güçlü testleri tercih edilir.
Bir istatistik testin yürütülmesinde bu varsayımları dikkate almak her zaman gereklidir. Standart testlerin bazıları veya aşağıdaki varsayımların tamamını gerektirir: dağılımının belirli bir formu, örneğin, verilerin normal dağılım olduğunu varsayarak; bu tüm veri noktalarını hiçbir mevsimsel değişiklikler veya veri diğer herhangi bir döngüsü bulunmaktadır ve böylece eşdeğer bir dağılıma sahip dağılım tutarlılığı ve bağımsızlık vardır. Ya da otokorelasyon, yani gelecek korelasyon bir zaman değeri ise geçen bu varsayımın ihlal edilmesi. Bu aynı zamanda seri korelasyon veya geçici korelasyon ya da bölgeler arasında özelliklede korelasyon bir çok bölge çalışması, mekansal ilişki söz konusu olduğunda adlandırılır.
İstatistiksel bir testte yapılan varsayımların verileri tarafından yerine getirilmemesi durumunda, o zaman test sonuçlarının önem düzeyi tahminleri kabaca hatalı olur bu anlamda anlamsızlık olabilir. Hidrolojik veriler genellikle açık olarak normal olmayan; Buna göre temel bir normal dağılım kabul testlerinin yanlış olacağı anlamına gelir. Hidrolojik veriler, otokorelasyon ve/veya mekansal ilişki de gösterebilir; Bu nedenle, veri değerleri bağımsız değildir. Bu eğilimin bir zaman serisi (Yue ve diğerleri, 2003) yeteneği üzerinde olumsuz bir etkisi olabilir. Verileri de mevsimsellik gösterebilir, bu dağıtım değişmezlik ile ilgili varsayımları ihlal ediyor. Testlerin gücü, zaman serisi değişkenliği, bir eğilim gibi test ediliyor özellikleri, büyüklüğü, dağılımı ve çarpıklık zaman serisi gibi örneklem büyüklüğü bağlı olabilir. Mann-Kendall ve Spearman'ın direnç testlerinin enerji sonuçları Yue ve diğerleri (2002) ve Yue ve Pilon (2004) tarafından sağlanmaktadır.
İstatistiksel testin ana aşamaları aşağıdaki gibidir:
(a) Kararı hangi ilgi konular bağlı olarak serisin/değişken tipini test etmek için verin, örneğin, aylık ortalamalar, yıllık maksimum veya mevsimsellikten arındırılmış verileri için;
(b) Değişim türleriyle ilgi neler olduğuna karar verin (eğilim/adım değişim);
(c) Veri varsayımları dışında örneğin araştırma verilerin analizleri kullanarak kontrol edin;
(d) Her değişiklik türü için uygun olan bir veya daha fazla test/değişim istatistikleri seçin; birden çok iyi bir uygulamadır;
(e) Anlamlılık düzeylerini değerlendirmek için uygun bir yöntem seçin;
(f) Önem düzeyleri değerlendirmek;
(g) Araştırmak ve sonuçları yorumlama.
Bir istatistik sınama seçilmesinin süreci iki bölümden oluşmuş olduğu kabul edilebilir: sınama istatistikleri ve sınama istatistiğinin anlamlılık derecesi belirlenmesi için bir yöntemi seçerek. Bu şekilde süreci görüntüleyerek mümkündür, bir sınama istatistiği seçmek için nasıl yapılacağını ve önem düzeyini değerlendirmek üzere birbirinden ayırt edilir.
Eğilim ya da hidrolojik verilerin diğer değişiklikleri için testlerin birçok yolu vardır. Yöntemleri belirli bir grup olarak dağıtımdan bağımsız metodlar olarak anılacaktır, varsayımlar için hangi verilerin elde edildiği dağıtım formu olarak gerekmez, örneğin, bu veriler normal dağıtılmakta olduğunu varsaymak gereksizdir. Aşağıdaki dağıtımdan bağımsız yaklaşımlar şunlardır:
(a) Sıra tabanlı testler: Bu testler, verilerin değerlerinin ancak gerçek veri değerleri arasına kullanın. Bir veri kümesi içinde rth büyük değeri ise bir verilerin kademe noktası r vardır. Çoğu kademe bazlı testler verilerin bağımsız ve aynı dağıtılmış olduğunu varsayıyorum. Kademe tabanlı testler, onlar genelde kullanımı kolay sağlam olduğundan avantajı vardır. Bunlar genellikle daha az güçlü parametrik bir yaklaşımı vardır.
(b) Normal-skorların dönüşümünü kullanma testleri: Değiştirmek için birçok testlerin normallik varsayımına güvenebilirsiniz. Bunlar genellikle çok normal dağılım olmakta olan hidrolojik veriler ile doğrudan kullanıma uygun değildir. Ancak, verileri öncelikle dönüşen bu tür testler kullanılabilir. Normal dağılıma sahip bir veri kümesi içinde normal puan dönüşümü sonuçlanır. Bir veriler serisinin saflarını kullanarak ama onun yerine onun kademesi r normal bir veri örneğinden rth büyük değeri olacağına tipik değeriyle değiştirilir, verilerin değerine göre veri değerinin değiştirilmesine benzemektedir (rth normal puan). Normal skorları kullanmanın avantajları, özgün verilerin normal bir dağılım uygulamasına gerek olmadığı göreceli sınama olacağı aşırı değerlere dayanıklıdır. Dezavantajı istatistik değişim ölçümü olmasıdır, regresyon aşaması gibi kolayca yorumlanamaz olmasıdır. Normal skorların testleri, büyük olasılıkla eşdeğer kademe bazlı testlere göre biraz daha güçlü olması muhtemeldir.
(c) Yeniden örnekleme yaklaşımlarını kullanma testleri: Aşağıda tanıtılan yeniden örnekleme yöntemleri, test istatistiğinin önemini belirlemek için verilerin kullanımı yöntemleridir.
Yeniden örnekleme yöntemleri, permütasyon testi ve önyükleme yöntemini bir sınama istatistiğinin önem düzeyi tahmin tekniklerinin sağlam bir dizisi vardır. Onlar esnek ve otomatik bağlantılı veya mevsimsel veriler dahil türleri çok geniş bir yelpazede adapte edilebilir ve göreceli olarak güçlüdür. Onların göreceli olarak az sayıda varsayımları aynı zamanda güçlü bir testtir ama veriler ile ilgili yapılmış olması gerekir çünkü yeniden örnekleme yöntemleri hidrolojik verileri test etmek için çok iyi şekilde faydalı oldular. Bunlar anlamlılık düzeylerinin sınama istatistiği için herhangi bir mantıklı seçimi konusunda tahminine izin veren esnek bir yöntem sağlar. Geleneksel istatistiksel testler anlamlılık belirlemek için sağlam bir yöntem kullanılarak hidrolojik bir dizi uygulaması için adapte edilmesini sağlar.
Yeniden örnekleme yöntemlerinin arkasındaki temel düşünce son derece basittir. Eğilim için bir dizi testleri ele alalım: regresyon geçişi mümkün bir denemedir. Verileri hiçbir eğilim (boş varsayımı) durumundaysa veri değerleri sırası az fark yapması gerekir. Böylece karıştırma veya suyun kirecinin filitrelenmesi, öğeleri veri serisinin geçişini önemli ölçüde değiştirmemelisiniz. Permütasyon bir yaklaşım altında çok sayıda veri karıştırılır. Sınama istatistiği, her karıştırmak veya permütasyon sonrasında yeniden hesaplanır. Birçok permütasyon sonrasında, orijinal sınama istatistiğini oluşturulan sınama istatistik değerleri ile karşılaştırılır. Orijinal sınama istatistiği üretilen değerleri önemli ölçüde farklıysa, bu verileri sıralama geçişini etkilemekte ve bir eğilim olduğunu göstermektedir. Daha sonra orijinal test istatistiği oluşturulan değerler ortasında bir yerde yatıyor, o zaman boş hipotez değerleri sırası önemli değildir ki doğru olduğu makul görünüyor; dolayısıyla trendin herhangi bir kanıtı yoktur. Başka bir deyişle, bu durumda bir gözlemci ya değer, istatistik sınama orijinal veriler ve yeniden örneklenmiş veya gözlenen veriler hipotezi tatmin etmek değil sayılırlar, değiştirilmiş verileri ayırt edebilirsiniz.
Önyükleme ve permütasyon yöntemleri iki farklı yaklaşımlar için yeniden örnekleme veri yöntemleridir. Permütasyon yöntemleri, herhangi bir örneklemede, verilerin her yeniden örneklenmiş veya oluşturulmuş verilerin serisi içinde sadece bir kez orijinal verilerin serisi içindeki veri noktalarından her biri yeniden sıralanır olduğu görülmektedir. Önyükleme yöntemleri, özgün veri serisi ile yeni bir dizi değerleri aynı sayıda yeni bir dizi vererek değiştirme ile örneklenir. Bu yöntem ile oluşturulmuş seri, orijinal serisi ve diğer değerlerin hiçbiri bazı değerlerden birini birden fazla kez içerebilir. Her iki durumda da, üretilen seri, gözlenen veri dağıtımı deneysel olarak aynı dağılım olarak gözlenir. Genel olarak, önyükleme yöntemleri permütasyon yöntemlerine göre daha esnektir ve çok çeşitli durumlarda daha geniş bir yelpazede kullanılabilir.
En basit örnekleme sırasını değiştirme veya önyükleme tek tek veri noktası için yukarıda açıklandığı gibi bir stratejisidir. Bu teknik, yalnızca bu verileri mevsimlik olmayan ve bağımsız olduğu kabul edilebilir olduğunda geçerlidir. Veriler mevsimsellik gibi bağımlılık veya başka yapı göstermesi durumunda, yeniden örnekleme tarafından oluşturulan serileri bu yapısının çoğaltılması gerekmektedir. Bunu gerçekleştirmenin basit bir yöntemi permute veya bloklar halinde verilerin önyükleme konumudur. Örneğin, aylık değerlerin 40 yıllık serileri için, onu bir yılın 40 bloktan oluşuyormuş gibi verilerini işlemek makul bir yaklaşım olacaktır. Her veri yıllık değer ve bozulmadan solundaki bir blok olarak beraber hareket ettirmek, böylece her bir yıl için mevsimsel ve zamansal bağımlılıklarını sürdürmek. 40 blok daha sonra birçok kez yeniden sıralanır. Bu şekilde, yeniden örnekleme serileri orijinal mevsimselliğini koruyacaktır. Benzer şekilde, bloklar verilerin otomotik bağımlılık (otokorelasyon) çoğaltılması için zorlanamaz. Bu blokların büyüklüğünün makul olarak seçilmiş olması önemlidir.
Mertebe bazlı testler gibi birçok serbest dağıtım testleri, bağımsızlık varsayımlarına bağlıdır. Eger bu varsayım geçerli değilse, hidrolojik bir veri için yaygın olarak tavsiye edilen yaklaşım ve bu test sonuçlarına dayanılarak yapılan sınama istatistikleri ayıklamak yerine bütün hatalara yol açabilecek anlamlılık için klasik formüller kullanmak yerine, blok önyükleme ve blok permütasyon (sırasını değiştirme) yöntemleri kullanılarak anlamlılığı değerlendirmektir. Mekansal bağımlılık bir grup olarak test edilir, çoklu konum veri kümesi varken bu yöntemler yararlı olabilir. Bu durumda, blokların her zamanki seçimi aynı zaman diliminde gerçekleşen tüm sitelerde grup verileri olacaktır (örneğin, Robson ve diğerleri, 1998).
Tablo II.6.1 değişim tespiti için standart ve parametrik ve parametrik olmayan testleri bunların temel özelliklerinin ve gerekli varsayımların bir özetini sunuyor. Testler standart şeklinde, yani yeniden bir örnekleme çerçevesinde açıklanmıştır. Bu testlerin her biri kolayca yeniden örnekleme testi olarak adapte edilebilir. Bunun için, sınama istatistiği bir test için hesaplanır, ancak hesaplanan anlamlılık düzeyi yukarıda açıklanan yeniden örnekleme yaklaşımı ile elde edilir. Sınama/testin seçimi için rehber Tablo II.6.2’de gösterilmiştir.
Yeniden örnekleme teknikleri kullanılacak ise, bu değişiklik belirli bir türü için test etmek için yeni sınama istatistikleri oluşturmak mümkündür-bilinen sınama/test istatistik yöntemini seçmenin gerekli olmadığı bilinmelidir. Özel sınama istatistikleri oluşturmak için esneklik ne test edilebilir ve nede büyük bir esneklik sağlar.
Test sonuçlarını yorumlarken, bütün sınama varsayımları yerine getirilmiş olsa bile tüm istatistiksel testin mükemmel olduğunu hatırlamak gereklidir. Bu nedenle, birden fazla testi kullanmasını tavsiye edilir. Yapmış olduğum bazı testlerin önemli sonuçları girerseniz, bu durumda birden çok anlamlılık değişikliği ek bir kanıtı olmadığını, bunların çok benzer olmadıkça bu değişimin daha güçlü kanıtlarını sunmaktadır.
Bu verilerin grafiklerinin yanında veriler hakkında mümkün olduğunca fazla tarihsel bilgi ile test sonuçlarının incelenmesi önemlidir. Örneğin, her iki adım değişikliği ve eğilim sonuçlarının önemli olup olmadığını, daha fazla bilgi bu değişimin en iyi açıklamasını sağlar ve bunların belirlenmesi için gerekli olacaktır. Tarihsel araştırmalar bir baraj döneminde inşa edildiğini ve işte bu barajın bir basamak değişikliğine neden olduğu sonucuna varmanın tespit edilmesi durumunda makul olacağını zaman serileri çizim ile tutarlıdır.
Test sonuçları, bir veri serisindeki önemli bir değişiklikler olduğunu ortaya koymaktadır, bu nedeni anlamaya çalışmak çok önemlidir. Her ne kadar iklim değişikliği saptamak için araştırmacılar ilginizi çekebilir, bunun incelenmesi gereken birçok başka nedeni olabilir (Kundzewicz ve Robson, 2004). Bu eğilimler bölgesel desenler gibi daha ileri yapı gösterebilir sonuçları modelleri dikkatli bakmak için yararlı olabilir.
Hidrolojik değişkenlerin göstergeleri için özel-rasgele alanlardaki zamansal kayma, örneğin, zaman serisi bir değişkeni bir dizi ölçüm değerleri kümesini oluşturabilir. Bir mekansal alanda veya mekansal noktaları bir dizi aynı zamanlı anlık bir değişkenin farklı gözlemlerini açıklayan bütün alanı kapsayan veriler uzaktan algılanır. Yağış gibi rasgele alanların mekansal yönlerini, yeraltısuyu seviyesi veya yeraltısuyu kimyasal maddelerin konsantrasyonları hidrolojide önemli konulardır.
Jeoistatistik alanında değişen miktarlarda istatistiksel olarak tahmin tekniklerinin kümesidir. Böylece kendisi de hidrolojik sorunları bir dizi için geçerli olma olasılığı ya da yeraltı suyu kalitesi gibi rasgele mekansal alanlara uygulamalar için çok uygundur (1992 Kitanidis bakınız). Jeoistatistik hidroloji ciddi öneme sahip birkaç pratik sorunlara çözümler sunmaktadır. Böyle birkaç komşu göstergeleri gelen gözlemlerine dayalı tahsis edilmiş bir yer için bir değer tahmin ya da düzensiz aralıklı yerlerde kıt bilgilere dayalı bir kontur haritası çizilmesi gibi enterpolasyonu kullanılabilir. Bu kümeleme sorunları çözebilir: alansal tahminleri bulma noktası gözlem noktası değerlerden alan olasılığının belirlenmesi ilkesini temel alır. Bu ağ tasarımının, örneğin, en uygun olan ağ genişletmesi, ağın ortak noktası veya ne yazık ki daha çok ağ azalması gibi izlenmesine yardımcı olabilir. Yeraltısuyu akım veya taşıma modelleri ile jeoistatistik kullanılarak, parametre tanımlama problemi örneğin gözlenen hidrolik geçirgenlik en başından belirlenerek çözülebilir.
Jeoistatistik yöntemle kriging tekniğinin temel sorunu bir bildirimde, z(x1), z (x2),…,z (xn) gözlemleri bazı ölçülemeyen konumu x0 bir büyüklüğün en iyi doğrusal bir tahminci arıyor (MAVİ) yerleri x1, x2, ..., xn bir dizi gibi formüle edilebilir:

Burada Z (x0) ile kestirim z (x0) ve i ağırlıkları vardır.
Sözde iç varsayımı altında tahmini varyansını ağırlıkları denklem 6,20 ve bir yarı variogram değerleri arasında ağırlıkları içeren matematiksel bir denklem yardımı ile ifade edilebilir. Ağırlık kümeleri olan tahmini varyansın az olduğu anlamında en uygun tahmini sağlamak şartı aranır. Kriging önemli bir avantajdır ancak sadece tahmin edilen değeri sağladığını aynı zamanda tahmin varyansı değerlendirilebilir konumundadır. Bu tekniğin çok işe yaradığını, burada gözlemlerin kullanılabilir bilgilerin yüksek maliyetli ve dolayısıyla kısıtlı ve en iyi organizasyon olması mevcut bilginin birincil öneme sahip olarak incelemesi den kaynaklanır.
Bugün jeoistatistik coğrafi bilgi sistemi ortamında dağıtılan modelleme ve enterpolasyon paketleri bir seçeneği için önemli bir unsur haline gelmiştir.