Hidrolojik Sistemleri ve Süreçleri Modelleme

[HOMS J04, K22, K35, K55, L20, L30]

Giriş

Hidrolojik döngü, dünyadaki suyun dolaşımı anlamına gelir. Farklı su depoları arasında su akıları bir dizi şeklinde oluşmaktadır. Hidrolojik süreçler içinde su akım örnekleri sıvı veya katı yağış, sızma, yüzey akış, kar erimesi, nehir akışı ve buharlaşma şeklşnde vardır. Karşılıklı su depolama örnekleri atmosferde bulunmaktadır; depresyonların, göletler, göller ve nehirler gibi arazi yüzeyinin; bitki örtüsü, toprak, akiferleri ve kar örtüsü gibi.

Tüm hidrolojik süreçler ve hidrolojik sistemlerin bazıları kütle ve momentum korunumu esasına göre katı fizik kanunlarından elde edilmiş matematiksel denklemler tarafından tarif edilmiştir. Diğerleri kavramsal yapısı veya bir kara kutu türü bulunmaktadır. Dinamik Hidrolojide kullanılan matematiksel denklemlerin kapsamlı bir değerlendirme Eagleson (1970) ulaşabilirsiniz. Bu bölümde bir kaç açıklayıcı örnekler yağışlar yüzeysel akış, akış yönlendirme, yeraltı suyu, su kalitesi, kar ve buz olaylarla ilgili içermektedir.

Tablo 1. Parametrik ve parametrik olmayan testlerin değişikliğini algılama, bunların özellikleri ve yapılan varsayımlar karşılaştırılması (izleyen Kundzewicz ve Robson, 2004 )

Test Adı	Ne Yaptığı	Özellikleri ve Yapılan Varsayımlar
Değişim için ortalama değişim noktası test/Pettitt's testi	Değişimi tam zamanlı bilinmeyen bir serinin ortalama bir değişikliği arama testi	Güçlü kademe-tabanlı test, sağlam dağılımsal formda yapılacak değişiklikler
Mann-Whitney testi/mertebe-toplam testi	Mann-Kendall test istatistiğine göre iki bağımsız örnekleme grupları arasındaki farklılıklar arayan test,	Kademe tabanlı test
Dağıtım içermeyen CUSUM (maksimum birikimli toplam) testi	Test içinde ardışık gözlemleri test istatistiği olarak ortalamadan farklılık işaretlerinin maksimum birikimli toplamı ile serisinin ortanca ile karşılaştırılmıştır.	Kademe tabanlı test
Kruskal-Wallis testi	Alt dönemin testleri eşitlik anlamına gelir	Kademe tabanlı test
Birikimli sapma ve diğer CUSUM testleri	Test ortalamadan sapmaları tekrar ölçeklendirilmelidir, birikimli toplamlar üzerine çalışmaktadır	Parametre testi, normal dağılım varsayımı
Öğrencinin t-testi	Testleri iki örnek farklı imkanlara sahip olmadığını - normal dağılım gösteren verilerin ve bilinen bir değişim noktası zamani varsayılmaktadır	Standart parametrik testi, normal dağılım varsayımı
Worsley olasılık oran testi	Uygun bir kullanım için değişim noktası zamanı bilinmediğinde	Normal dağılım Öğrencinin t-test, benzer varsayım
Eğilimi Spearman rho Testleri	Zamanı ve mertebe serileri arasında korelasyon için testi	Kademe tabanlı test
Kendall's tau/Mann-Kendall testi	Spearman rho benzer şekilde, ama herhangi parametrik analog ile ilişki için farklı bir ölçüm kullanmaktadır	Mertebe-Tabanlı Test - mevsimsellik sağlayan genişletilmiş testler, örneğin, Hirsch ve Slack (1984)-ve otokorelasyon
Doğrusal regresyonu	Normal olarak bir test olarak regresyonu eğimi kullanan bir test istatistiği	Bir varsayım, normal dağılım eğilimi için en yaygın kullanılan testlerden biri
Not: Tüm testlerin verileri aynı şekilde dağıtılmış olduklarını ve bağımsız bir varsayım yapmak.

Hidrolojik modelleme daha bütünleştirilmiş bir model için daha fazla katkıda bulunmaktadır. Hidrolojik akış simülasyonu ötesinde, bütünleştirilmiş modeller toprak erozyonu, nehir sediment, ekohidroloji, bitki verimi ve ekohidroloji gibi diğer disiplinlerin, iklim etki değerlendirmesi ve su yönetimi ile arabirimleri bulunmaktadır.

Yağış-akış ilişkileri

Genel

Yağış-akış ilişkileri tasarımı, öncelikle tahmin yürütme ve değerlendirme için kullanılır. Akım verileri kullanılamıyor veya bir yorum için güvenilirliği çok sınırlı ise, yağış-akış ilişkileri yağış miktarı kayıtlarından akım bilgi elde etme yeteneği nedeniyle son derece yararlı olabilir. Göreceli basitliği ve yağış miktarı verilerinin toplanmasının düşük maliyetli olması özelliğinden dolayı, genellikle daha bol miktarda akım verileri vardır. Eğer ilgi havza için yağış miktarı ve yüzeysel akış arasında güçlü bir ilişki kurulmuş olabilirse, yağış miktarı-yüzeysel akış ilişkisi olabilir yağış miktarı verilerinin kombinasyonu, örneğin, ya da bölgesel bir sel ilişkisi (Bölüm 5) ya da havza gelen zayıf akım verilerinin bir bilinene dayanan tahmin daha yüksek akim sıklığı daha güvenilir tahminler verir.

Genel olarak, yağış miktarı-yüzeysel akış ilişkileri iki ayrı aşamada geliştirilir: belirli miktardaki yağış sırasında belirli bir dönem sonuçları akış hacmi ve yüzeysel akış hacmi dağıtımının zamanıda belirlenmesi. İlk adım evapotranspirasyon, sızma ve yüzeysel akış arasındaki yağışların bölümlendirme nedeni ile gerekmektedir. (bkz: Cilt I, Bölüm 4). İkinci adım, varış zamanı ve yağış miktarı tarafından oluşturulan yüzeysel akışın dalgasının zayıflaması için hesap gerekmektedir. Bu bölümün geri kalanında bu iki adımı tartışılması oluşturmaktadır.

Akış hacimleri

Önceki yağış indeksi

Yağış rejimi endeksi öncelikle nehir tahmini için geliştirilmiştir ve geniş bir drenaj alanları ve koşullarına uygulanır. Belirli bir drenaj alanı için onun türetilmesi gözlenen yağış miktarı ve yüzeysel akış verileri biraz zaman aralığını gerektirir. Bu şekilde tanımlanmıştır:

Burada Io endeksin başlangıç değeri olduğu, k bir durgunluk faktörüdür, t hesaplama için zaman aralığı, Pi zaman aralığında meydana gelen günlük yağış sayısı ve t(i) yağışlı gün tarihinden itibaren geçen günlerin sayısıdır.

Genellikle yağış rejimi endeksi basit formları kullanmak daha uygun olur. Bir veya daha fazla değişkenlerinin belirli havzalarda ihmal edilebilir bir etkiye sahip olabilir ve bu değişkenlerin sayısını azaltmak daha sonra mümkün olabilir. Ancak, her durumda genel yöntemi aynıdır.

Bitki örtüsü, toprak tipi ve diğer önemli havza özelliklerinin yanı sıra yılın süresinin etkisi durgunluk faktörünü yansıtılmaktadır. Yılın zamanlı güneş enerjisinin, bitki durumu ve buharlaşma ve su toplama havzasındaki nem terlemesini etkileyen diğer faktörlerin mevsimsel eğilimini temsil eden eğriler bir aile olarak ifade edilir. Öncül yağış indeksi havza içindeki nem ve topraktaki nemin bir ifadesidir.

Şekilde II.6.6 yağış rejimi endeksi için 0,9 günlük durgunluk faktör davranışı örnek gösterilmiştir. Bir drenaj alanındaki yağış rejimi endeksi birkaç istasyon için ortalama yağış miktarı ya da her istasyon için tek tek olacak şeklinde hesaplanıyor olabilir. İkincisi sıklıkla tercih edilir.

Tablo 2. Test seçim kuralları

Durum	Hangi Test Seçileceğini Belirleyin
(a) Veriler normal dağılım ve bağımsız.	Bu hidrolojik veriler için sıradışı bir senaryodur. Varsa, Tablo II.6.1 listelenen testlerden herhangi birsi uygun olmalıdır.
(b) Veri normal olmamakla bitlikte mevsimselde değildir veya bağımsızdır.	Serbest dağıtım testlerinden herhangi biri uygundur. Normallik varsayımına dayalı testler de ilk normal skorları veya sıra sayıları dönüşüm uygulayarak ya da alakalı sınama istatistikleri kullanılarak ve yeniden örnekleme tekniklerini kullanıyorsanız önemini değerlendirilmesi ile uygulanabilir.
(c) Veri normallik olmamakla bitlikte bağımsızda değildir veya mevsimsellik vardır.	Veri yukarıdaki verilen temel testlerin herhangi biri için varsayımları karşılamaz. Bu ve sınama istatistikleri ayıklamak için blok permutasyonu veya blok önyükleme yöntemleri kullanıyorsanız anlamlılık düzeylerinde değerlendirilmesi gerekmektedir.

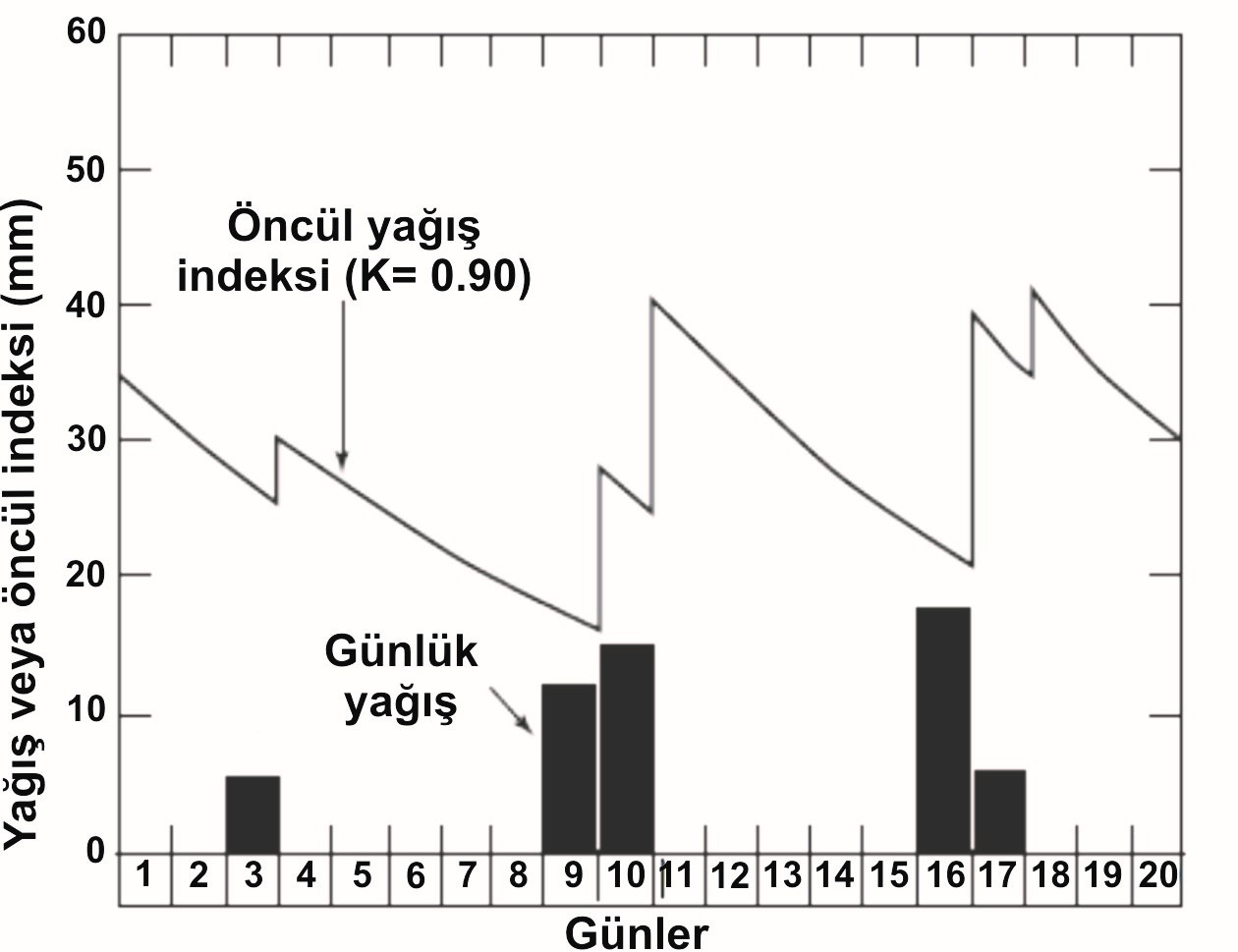
Şekil 6. Öncül yağış indeksi

Şekil 7 yağış tahmininde yüzeysel akış hacminin yöntemini ve yağış rejimi endeksi gösterilmektedir. Kesikli çizgiler ve oklar bu diyagramın kullanımını göstermektedir. Örneğin, diyagram yağış rejimi endeksi için 22 mm değeri ile girildiğinde. Uzun çizgi ve oklar Temmuz ayı ve 24 saatten fırtına süresinden aşağısı için yol gösterir. Örneğin sonra drenaj alanı üzerinde 16 mm ortalama derinliği bir yüzeysel akış öncesine kadar 40 mm ve varsayılan fırtına, yağış durumuna sağa doğru ilerler.

Yukarıdaki örnekte varsayımsal fırtına Şubat ayında gerçekleşmiş olsaydı, diğer koşullar aynı olmak kaydıyla 22 mm öncül yağış etkisinin farkı olacaktır. Normalde Şubat ayında, Temmuz metodlarıyla, öncül yağış aynı miktarda toprak neredeyse hareketsiz bitki örtüsü ve kış aylarında daha az su tüketimi nedeniyle doymuş şekilde olurdu. Kısa kesik çizgi ve oklar Şekil II.6.7 de İkinci örnekteki 40 mm yağmurdan gelen yüzeysel akış 30 mm, dolayısıyla Temmuz ayında neredeyse iki kat yüksek olacağını gösteriyor.

Donmuş toprak ve kar birikimini öncül nem koşullarının tahmin edilmesinde özel bir dikkat gerektirir. Donmuş toprak ile maksimum yüzeysel akışı veren yılın belli zaman eğrisi yaygın olarak kullanılmaktadır. Zemindeki kar etkisi, düzgün toplam birikiminin yerine erime oranı ve miktarı açısından ifade edilir. Kar erimesi 6.3.5 tartışılmıştır.

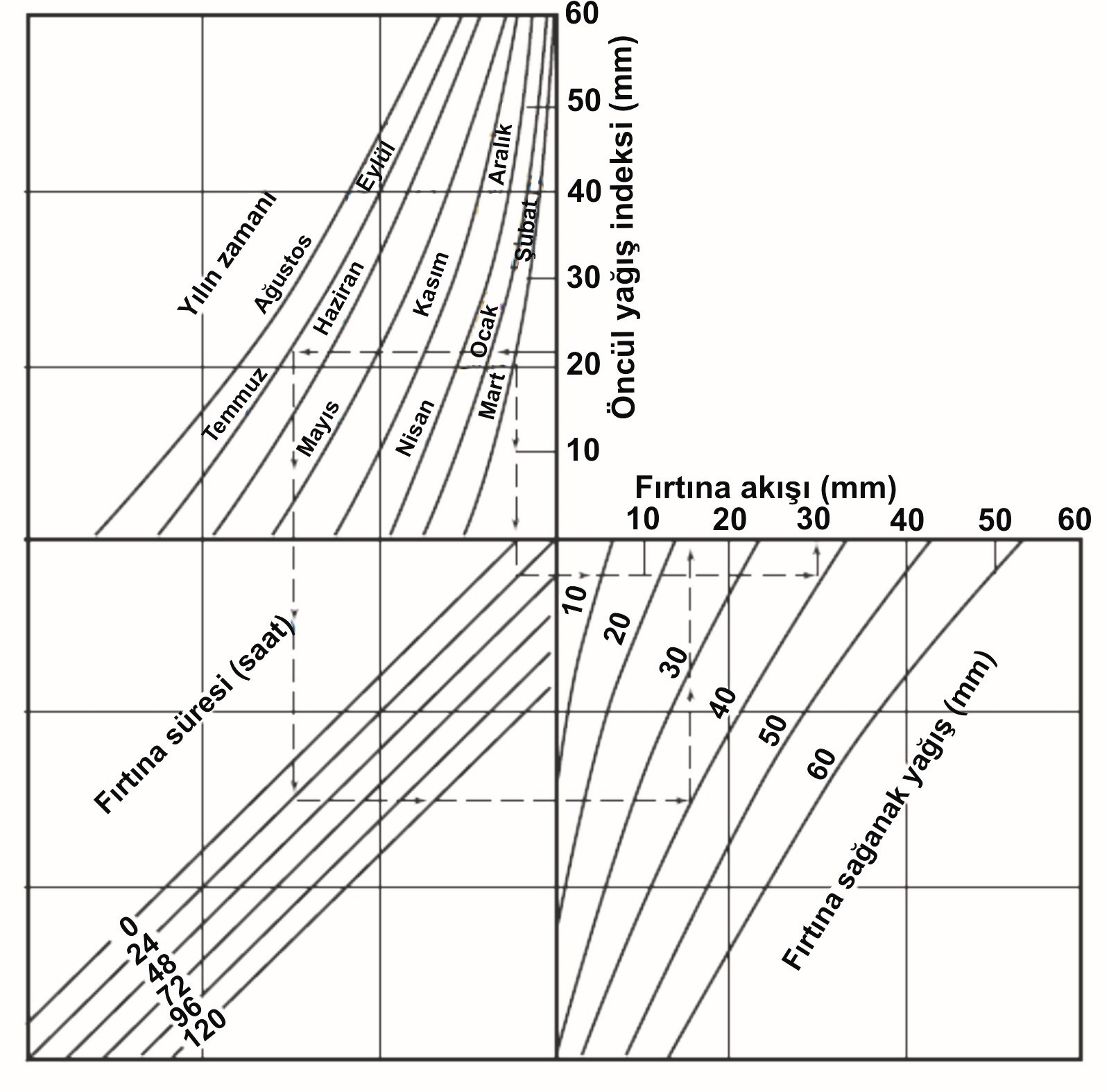
Şekil 7. Öncül yağış indeksi kullanarak yağış yüzeysel akışın tahmini

Yüzeysel akış hacmi için bir dizin gibi başlangıç temel akımı

Nemli bölgelerde, burada genellikle ilk havza koşullarının bir göstergesi olarak kullanılan bir sağınağın başlangıcında yeraltı suyu deşarj biçiminde kuru taban akışı havza koşulları sık sık kullanılır. Bu tür ilişkinin bir örneği Şekil II.6.8 gösterilmiştir. Temel akışı deşarj tüm alan boyunca koşulları yansıtmaktadır. Bazı bölgelerde, bu durun sezon ile ilişkiyi değişiklik için gerekli bulunmuştur. Yaz ve kış, mevsimler arasında oluşan sağınak olaylarının kaçınılmaz sorunlarına yol açan bir ilişki geliştirmek bakımından yaygın bir yöntemdir. Her zamanki bir çözüm her bir eğri temelinde yüzeysel akış tahmini yapmak ve daha sonra enterpole etmektir.

Yüzeysel akış koşulları için bir dizin olarak başlangıçtaki yeraltı suyu deşarj kullanımı genellikle kısa konsantrasyon süreleri olan küçük havzalar ile sınırlıdır. Yağışlı bir sezon daha büyük alanlarda hidrograf bir yükselişi ilk yeraltı suyu deşarj tespitini zorlaştırır son bindirilen eğilimindedir. Her zamanki yaklaşımı, ilk yeraltı suyu deşarj için küçük dizin havzaları belirlemeye ve hidrolojik benzer özelliklere sahip yakındaki diğer yakın bölgelerine uygulanacak şeklindeki yaklaşımdır.

Nem hesaplama teknikleri

Toprağın nem eksikliği toplam yağış miktarı ve yüzeysel akış arasındaki ilişki açısındaki en önemli faktördür. Bir alan için başlangıçtaki toprak nem eksikliği, tahmin etmenin uygulamalı bir anlamı ortaya çıkan yüzeysel akış için sağanak yağış miktarı ilişkilendirilmesi bakımından bir prosedür eklenmesi için çok kullanışlı bir değişken sağlayacaktır. Belirli bir toprak profili için toprak nemi ölçmek için aletleri ama oldukça pratik hale gelmiştir hatta küçük bir havzada mevcut toprak profilleri ve nem koşullarının çok çeşitliliği bir yağış-akış ilişkisinde tartışmalı değerinin toprak nemi bakımından ölçümlerini sağlar.

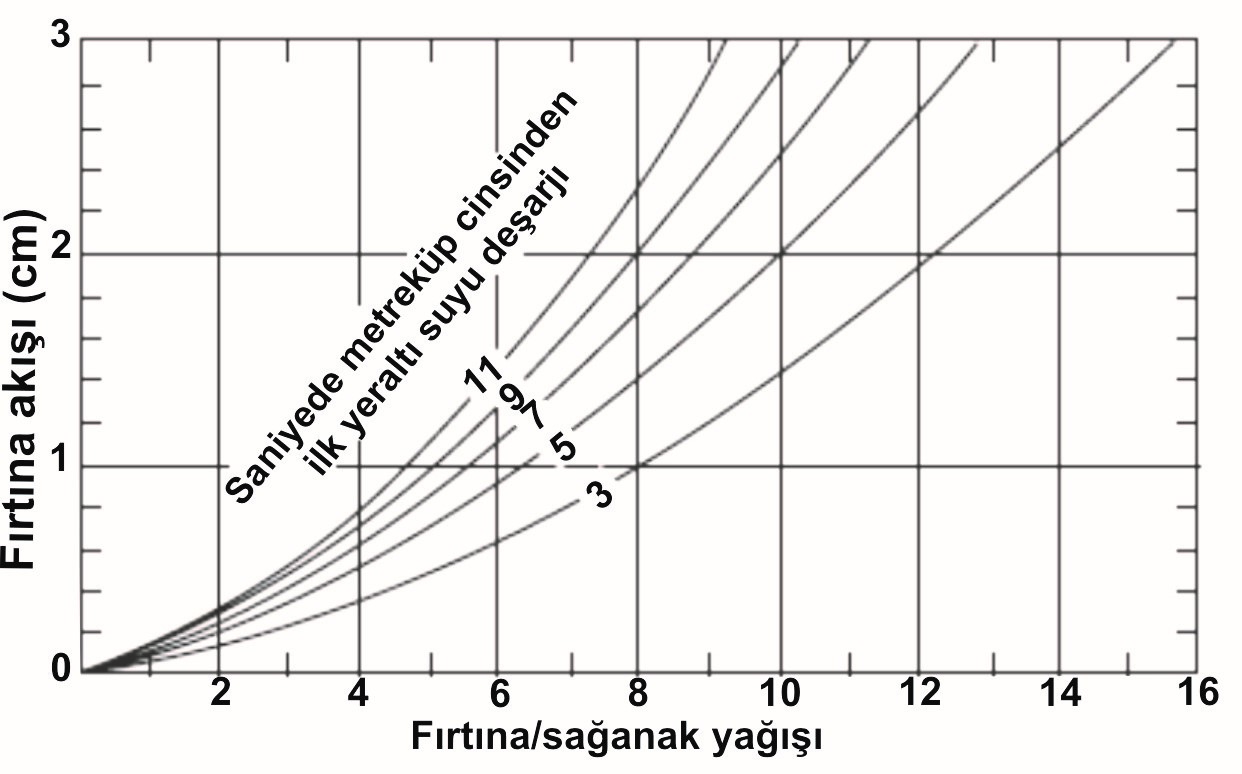
Şekil 8. Yağış-akış ilişkisinin bir göstergesi olarak kabul tabanı akımı

Daha fazla umut verici bir yaklaşım toprak neminin sonuçları bütün bölge ile ilgili değerleri bir alansal hesap tekniğinin kullanılmasıdır. Böyle bir yaklaşımda, yağış giriş ve çıkışının akım kanalı ve bitki su tüketimi atmosfere toprak ve bitki yüzeylerinden tarafından alandan çıkış, yüzeysel akış oluşuyor. Alan üzerinde yağış tahmini aracılığıyla noktalı değerler arasında mekansal ortalamaların oluşturulması sırasında en sık rastlanan bir sorundur. Alandan yüzeysel akış akım kayıtlarından tespit edilebilir. Sorun neden belirli fırtına akışına uyan biri şekline gelir (bkz: 6.3.2). Farklılık, yağış eksi yüzeysel akış ve alandaki kalıntıların yeniden şarj olarak adlandırılan suyu ifade eder, Rc.

Üçüncü unsur, bitki su tüketiminin doğrudan ölçümü son derece zor olduğu için değerlendirmesi en zor öğedir. En fazla toprak nemi hesap teknikleri gerçek bitki su tüketimi potansiyel evapotranspirasyon, ETP ve toprak nemi rejimlerindeki eksiklikler şeklide basit bir ilişki taşıdığı temel dayanak olarak alınmaktadır.

Toprak nem hesap basit bir formu olan toprak profilini bütün alan üzerinde bir kapasitesi, S, olduğu kabul edilir bir durumdur. Toprak nem eksikliği, DUs, sonra aşağıdaki denklem tarafından belirlenir:

Burada DUs(t) t zamanında toprak nem eksikliği, DUs(t + 1), bir süre sonraki değerdir, Rc yağış ve/veya kar erimesinden kaynaklanan yeniden şarj olduğunu ve ET oluşursa t ve t +1 arasında gerçekleşen bitki su tüketimi olduğunu. Eksikliği sıfır sınırları ve S arasında değişir.

Bu yaklaşım evapotranspirasyon (S-DUs(t))/S oranı ile çarpılarak daha gerçekçi hale getirilebilir, böyle olduğu gerçek bitki su tüketimi toprak profilinde mevcut nemin temini ile birlikte azaltmakta olduğunu kabul ediyor.

Başka bir olası değişiklik toprak profilini katmanlara bölmek istiyorsunuz. Bu yaklaşımda, bu üst-katman nemin birinci alt tabakasının incelmesi herhangi bir şekilde önceden tüketilmiş olması gerektiği kabul edilir ve tersine, alt katmana şarj üst katmandan taşması ile sınırlıdır olması kabulü varsayılmaktadır.

Bir yağış miktarı-yüzeysel akış ilişkisinin toprak neminin hesap değerlerinin uygulaması hesaplanacaktır, boşaltmak için Q yüzeysel akış ilgili olarak kullanıcısı tarafından yapılabilir:

Q = cQU + (1 – c)QL (6.23)

Burada c sabittir, QU yukarı katmandan hesaplanan yüzeysel akış ve QL düşük katmandan hesaplanan yüzeysel akış olduğunu gösterir.

Yüzeysel akışın zamansal dağılımı

Havza çıkışında zaman içerisinde seyahat zamanı ile bir yağış miktarı olayı bir havzada uygulanan hesaplamada su hacminin zayıflamasını/emilimini hesap etmek için yapılması gerekmektedir. Bu adım genellikle havza terkedildiğnde yüzeysel akışın zamansal dağılımını açıklayan bir birim hidrograf kullanımı ile gerçekleştirilir. Birim hidrograf aşağıdaki şekilde kütle devamlılığı ilkesi ile sınırlıdır:

V = Q(t)dt (6.24)

Burada Q(t) anlık deşarj oranıdır, t zaman ve V yüzeysel akış hacmidir. Fonksiyonu Q (t) olan şeklinde doğru bir şekilde havza özellikleri temsil eden bir eğri tanımlamaktadır. Karşılaştırma farklı havzalar için hidrograf ve sentetik hidrograflar hazırlanmasında yardımcı elaman için, hidrolojik ve meteorolojik yazmasını hidrograf özellikleri ilgili belirleyici/deterministik modeller geliştirilmiştir. Bu modeller, aşağıda açıklanmıştır.

Birim hidrograf

Etkili yağışın birimi sonucunda akıntı hidrografının zamanı belirtilen dönemi boyunca tek bir oranın de havza genelinde standart olarak üretilen bir havza için birim hidrografı tanımlanmaktadır. Uygulamada, birim hidrografın zamanla değişmez olduğu kabul edilmiştir. Daha sonraki başka bir birim yüzeysel akış hacimleri ile birlikte etkinlik birim hidrograf ile orantılı olup hidrograf teorisi üretimi varsayılmıştır.

Akım kayıtlarından türetilmesi

Belirli bir yağmur fırtınasından gelen akış hacmini belirlemek için hidrografın ilgili bileşenlerine ayırmak gereklidir. Tek bileşenli belli bir fırtına ile birlikte ilişkili doğrudan ya da fırtına yüzeysel akış konumundadır. Akarsu akışının devam etmesinden gelen akış için önceki katkıları, bir başka önemli bileşenlerinden biridir. Üçüncü önemli bileşeni zemin geçirerek gecikmesi daha önceki fırtınaların akış bileşenidir. Bu bileşen yeraltı akışı olarak bilinir, başka bir deyişle, biraz gecikme ile toprağa geçerek suyun genellikle doğrudan bir yüzeysel akışın bir parçası olarak dahil edilir. Akım sürekli simülasyon için daha fazla güncel kavramsal modellerin bazıları ayrı ayrı yukarıdaki bileşenlerin her işlem için hükümleri vardır.

Bu tür bir analiz gözlenen hidrografı inceleyerek her bileşenin belirlenmesine izin vermez. Içinde yalnızca iki bileşenli tanınan analizleri daha az karmaşık yöntemler olarak, gözlemlenen hidrografın farklı ve iki bileşenden büyüklüğünün değerlendirilmesi mümkündür. Aşağıdaki örneklemede, doğrudan akış hem de yüzeysel akış ve toprak altı akışını içermektedir.

Onun önemli bileşenleri içine bir hidrografının ayrılması için çok sayıda yöntemleri en basit bir tanesi Şekil II.6.9. de gösterilmiştir. Temel akışın izlemesinin yaygınlaştırılması (bkz: çizgi parçasının AB) akışın zaman içinde yükselmeye başlamadan önce onun eğiliminin genişletilmiş kısımdaki tepe akımı. B noktasından itibaren, daha sonra bir sabit zaman itibariyle noktayı c hidrograf kesiştiği için düz bir çizgi çizilir. B den C'ye kdar geçen süresi olarak büyük oranda drenaj alanının büyüklüğüne göre belirlenmektedir. Genellikle hakkında (A / 2) 0.2 'dir, burada A kilometre karelik drenaj alandır.

Hidrografının ayrıştırlmasında çeşitli yöntemler yaygın olarak kullanılmaktadır. Aynı tekniği, gerek uygulamada ve gerekse geliştirmede kullanılmalıdır, ancak, daha fazla yöntem daha önemli bir olan gerekliliktir.

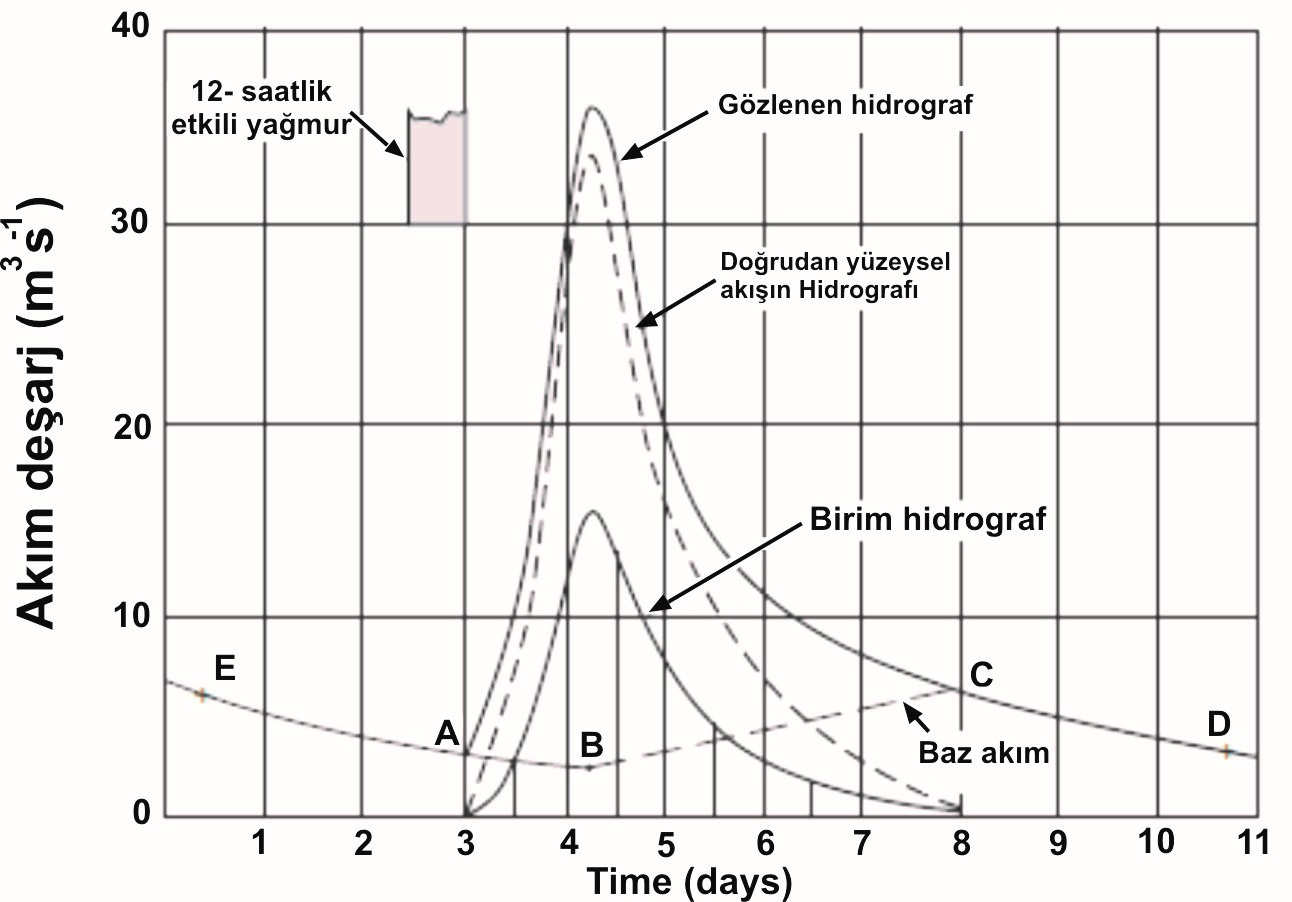
Şekil 9. Hidrograf analizi

Belirli bir fırtınanın veya fırtınalı bir dönemde ile birlikte ilişkilendirilmiş toplam akış aşağıdaki yöntemi ile tespit edilebilir. Başlangıç ve bitiş noktaları aynı yeraltı suyu durgunluk koşulları ve bu nedenle, aynı depolama temsil etmektedir çünkü Şekil II.6.9 olarak kere A ve D arasındaki hidrografın altında alanında fırtına yüzeysel akış konumundadır.

Şekil 32. gözlenen verilerden doğrudan akım birim hidrograf türetmeniz için gerekli adımları göstermektedir. Bu adımlar, grafik veya sayısal olarak gerçekleştirilebilir. Doğrudan yüzeysel akışın hidrografının ABC izleme değerinin üstündeki akışıdır. Doğrudan yüzeysel akış hacmi hidrografının altındaki alanda entegre edilerek elde edilir. Bir planimetre mevcut değilse, uygun bir yöntem, karelerin sayılması yöntemidir. Bu varsayımsal örnekte, doğrudan yüzeysel akış hacmi 4 320 000 m3 olarak bulunmuştur. 200 km2 lik bir varsayılır drenaj alanı içinde, bu hacim 2.16 cm ve ortalama derinliği temsil etmektedir. Birim hidrografının elde etmek için kendisine gerekli konumundadır, 2.16 ile doğrudan yüzeysel akış hidrografının her biri düşey koordinatlara bölmek, böylece belirlenen hidrografının drenaj alanı üzerinde doğrudan yüzeysel akış alanı, diğer bir deyişle, birim hidrograf üzerinde yol açacağı hidrograf şeklini gösterir.

Bazı havzaların kayıtlarında, bu birimi veya akarsudaki yükselir diğer olayların komplike üretimi için tek fırtına bulmak zordur. Bu gibi durumlarda, bir birim hidrografın türetilmesi daha fazla karmaşık hale gelir. Bu şartlar altındaki bir birim hidrografının türetilirken bir yöntemi ve ilk birim hidrografının üstlenmeye ve tahmini yüzeysel akış artışlarını kullanarak çeşitli fırtınalar için doğrudan yüzeysel akışın hidrograf teorisi yeniden inşa etmek gibi sonuçları ile gösterilen ardışık yaklaşım ile birim hidrografının hassaslaştırmasını sağlamaktır. Bu yeniden yapılanma yöntemi, Şekil II.6.10 tarafından gösterilmiştir:

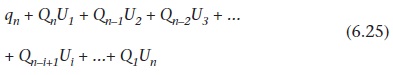
Burada qn doğrudan akış zamanında n gelen akıntı oranıdır, Ui i-birimi hidrograf koordinesi ve Qn-i+1 aralığı için doğrudan akış olduğunu gösterir. Bu denklem aynı zamanda en küçük kareler tarafından birim hidrograf türetme için regresyon modeli olarak kullanılabilir.

Drenaj alanları için 200 ile 2 000 km2 ye kadar altı saatlik zaman aralığı olarak kullandığınız birim hidrograf gelişimi için yaygın olarak kullanılır, ancak yüksek doğruluk için kısa zaman aralıklarla olanları kullanılabilir. Küçük drenaj alanlarında da kısa zaman aralığına sahip artışlı olanları gerektirebilir. Zaman artışları yeterli hidrografının şekli iyi bir tanım vermek için ve izin verilen aralık çok fazla geniş bir zaman aralığını kapsayacak şekilde yapılır bir tahmin küçük aralıklarda olmalıdır. Drenaj alanları yaklaşık 2 000 km2, daha geniş bir zaman artışları birim hidrografı kullanılabilir, daha büyük olan ama bir kural olarak birim hidrograf teorisi ve kollarından bölgelerine uygulanması gereken yönlendirme ile kombine edilebilir.

Kanal hidroliği değerlendirmelerinde tahmin edilebileceği gibi, yüzeysel akış büyüklüğü ile birlikte artışı için birim hidrograf ile zirveye çıkma durumu için bir eğilim vardır. Buna göre, uygulamada, birim hidrograf bir ailenin ikinci tur seçimlerinin az miktarları için akış ve daha düz tepelerde geniş miktarlardaki durumlar için daha yüksek zirve birim hidrograf teorisi ile birlikte, belli bir havza için kullanılabilir. Çoğu kez sadece iki kategoride aile oluşturmaktadır.

Birimi, hidrografının kullanımında beceri çalışma ve uygulamalardan elde edilir. Bu bölümde açıklananların dışında başka yöntemler ve iyileştirmeler için referans kitapları ve rutin olarak düzenli operasyonlarda el kitapları kendi normal işlemlerde birim hidroğrafları düzenli olarak kullanan kuruluşlar için başvuru yapılabilir.

Yapay yöntemlerle türetilmesi

Genellikle bu yapılar ya da operasyonlar ölçülmemiş akarsu planlaması için çoğu zaman gereklidir. Bu gibi durumlarda, bir yapay birim hidrograf teorisi (Dooge, 1973) geliştirmek için yararlı olur. Bir birim hidrografının yaygın olarak kullanılanın türetilmesi hangi havzalarda ve birim hidrograf teorisi çok sayıda birim hidrografının ve drenaj havzasının nesnel fiziksel özellikleri şeklinde arasındaki ilişkileri türetmek için analiz edilmiş ve Snyder tarafından elde edilen bir yöntemdir.

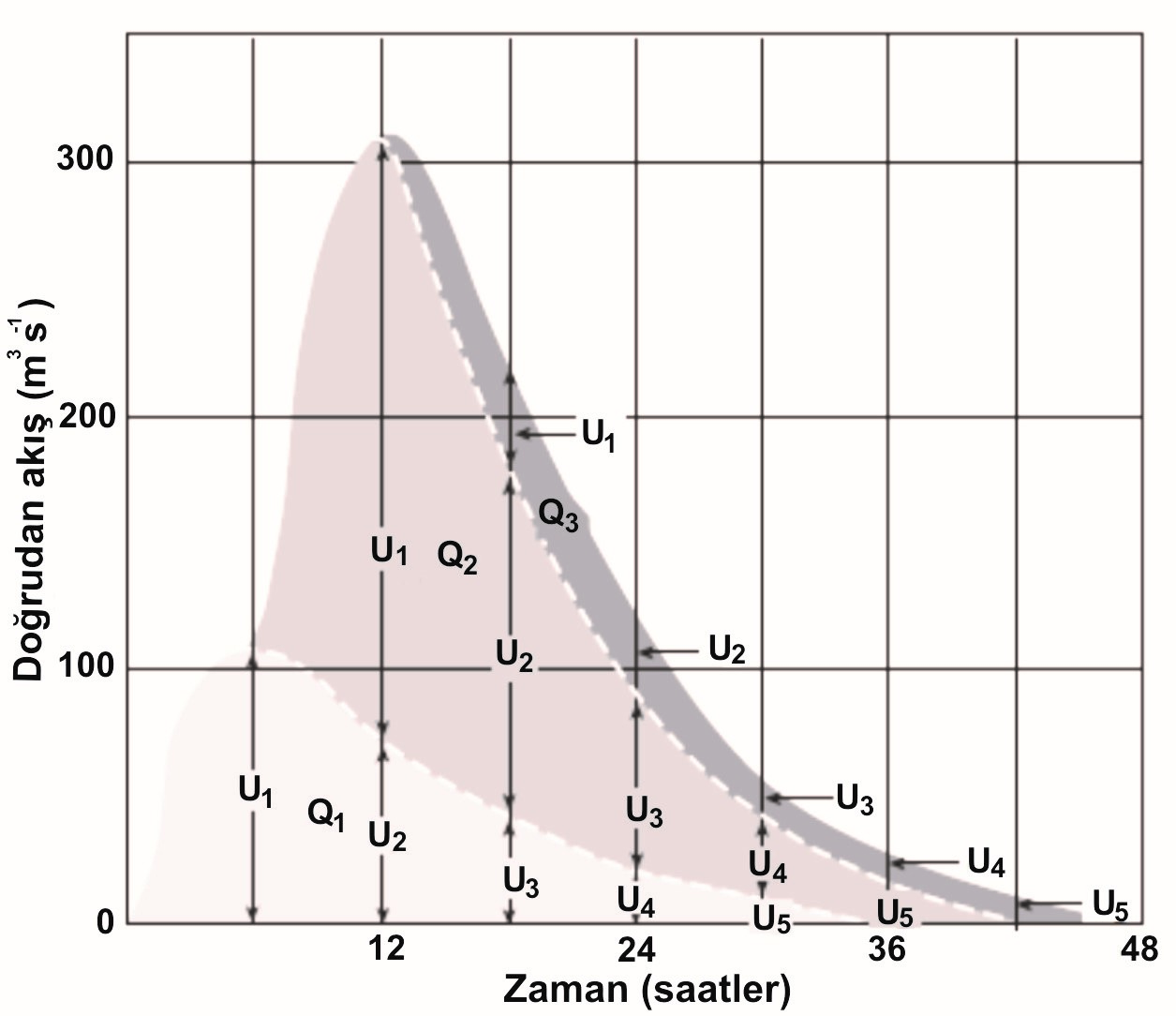
Şekil 10. Doğrudan akış hidrografının yeniden inşaası

Bir birim hidrografın, onun zirveye yapma durumu, tabanının uzunluğu ve çeşitli şekillerde tanımlanabilir havza gecikmesi şeklindeki önemli parametreleri vardır; Burada, hidrografının ancak tepesi için ağırlık merkezi itibaren yağış zamanıdır. Snyder'ın yöntemde, havza gecikmesi, tp, saat içinde verilir:

Burada C1 birimlerini dönüştüren ve deneye dayalı bir katsayısı, l kilometre olarak ana akım uzunluğu, lc çıkış ve n drenaj alanının ağırlık merkezi arası kilometre cinsinden mesafedir deneysel bir üstür.

Birim hidrografın zirveye çıkma durumu için, bu yöntemin C2 deneye dayalı olmak üzere yağmur, tp/C2 standart bir süre kullanır. Yağmurlar, bu süre için:

Burada Qp akış m3 s-l içinde pik hızı, C3 deneysel bir sabit, km2 içindeki bir drenaj alanı ve tp bir saat içinde gecikmesi. Tb olduğu gibi gün olarak zaman tabanı aşağıdaki gibidir:

Sabitler d ve C4, temel akışı doğrudan akıştan ayırmak için kullanılan yordam tarafından sabitlenir.

Yağmurun standart süreleri dışındaki TR süreleri için karşılık gelen gecikmesi, tc, aşağıdaki gibidir:

Burada f (TR) süresinin bir fonksiyonudur.

Snyder'ın katsayıları, Amerika Birleşik Devletleri Appalaş Dağları akışları için elde edilmiştir. Genel yöntemler diğer bölgelerde uygulanabilir bulunmuştur ama farklı katsayılar topografya, jeoloji ve iklim farklı türleri için beklenemez.

Rodriguez-Iturbe ve Valdes (1979) jeomorfoloji ve iklim özelliklerinden deneysel yasaların yardımıyla bir anlık birim hidrografı sentezlemek için bir fiziksel tabanlı yöntem geliştirilmiştir. Daha sonra jeomorfolojik iklimsel anlık birim hidrografı olarak bilinen jeomorfolojik anlık birim hidrografını önerdi. Onlar da en yüksek akış düzeni ve akış hızı ve çatallanma oranı, uzunluk oranı, alan oranı, uzunluk fonksiyonları gibi jeomorfolojik anlık birim hidrograf zirvesindeki pik ve zaman değeri için eşitlikler geliştirilmelidir.

Birim hidrograf sürelerinin dönüştürülmesi

Birim süresinin uygun bir yağış miktarı nadiren gözlenmiştir. Toplam tutarı ve yağmur süresi tamamen aynı olabilecek ancak, zaman ve mekan olarak yağış miktarı değişimleri, farklı hidrograflar teorisi üretir. Bu nedenle, genel bir birim hidrograf türetilmesi birçok birim hidrograf teorisi bir ortalamasını gerektirir.

Birim hidrograf teorisi yaygınlaştırmak için bir tekniği farklı sürelerinin birim hidrograf teorisi karşılaştırılması gereğidir. Süreleri t saatlik bir birim hidrografın kendisi eklenirse, gecikmeli t saat ve eksenleri iki bölümlendirilmeyle bir birim hidrografın 2t saat sonucu olduğudur. Benzer dönüşümleri görülmektedir.

Değiştirmek birim hidrograf teorisi için bu temel fikir daha geniş bir uygulamanın toplamı ya da S-eğrisi yöntemi olarak bilinmektedir. S-eğrisinin t saatte bir santimetre yüzeysel akış artışlarla sonsuz bir serisinden ortaya çıkacak hidrograf konumundadır. Bu birim hidrograf teorisi her bir önceki bakımından T saat gecikmeli bir dizi ekleyerek inşa edilmiştir. Birim hidrograf için T saatlik bir zaman tabanı ile, t saat için doğrudan bir yüzeysel akış birisi santimetre üreten kesintisiz yağmurda T saat sonunda sabit bir çıkış geliştirmek şeklinde olacaktır. Bu nedenle, T/t saat denge akışı bir S-eğrisinin üretimi için gerekli olacaktır.

S-eğrisi yapımı grafiksel bir prosedür yerine, sayısal olarakta gerçekleştirilebilir bir yöntemdir. Bir birim hidrograf için herhangi bir süre t s-eğrisinin t saat geri kalmış ve gecikmeli ve gecikmesiz S-eğrilerini koordineli almak suretiyle elde edilebilir. Birim hacmi elde etmek için aşağıdaki koordinatları t saat orijinal birim hidrograf uygulanma süresi oranı ile çarpılması gerekir.

Anlık birim hidrografı olan zaman birimi, t, sonsuz küçük birim hidrograf konumundadır. Bir anlık t-saatlik birim hidrografı yapımı bir S-eğrisi vasıtasıyla yapılır.

Izokron/Eşhacim yöntemi

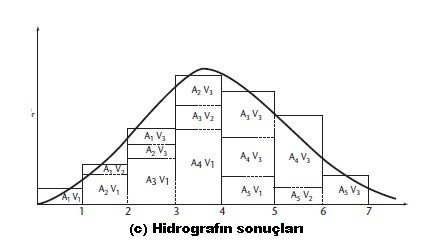
İzokron/eşhacim yöntemi bir havza akarlarının birinci kavramlarından birinin ifadesidir. Bir drenaj avzası farklı kısımları arasında meydana gelen akım, farklı zamanlarda akışı içinde bir noktaya varır. Birinci su akışı yükselmesi genellikle havza çıkışına yakın bölgesinden havzası terk etme sırasında gelmektedir. Daha sonra, su ve havzanın orta kısmında geniş alanlarında meydana gelmektedir, son olarak, su drenaj alanının uzak bölümlerinden geliyor. Böylece, drenaj havzası içinde hangi su ölçüm noktalarındaki sırayla ölçümlerde suyun gelişine göre bölgelere ayrılabilir. Şekil II.6.11 (a) bu bölgelerin bölünmesini sağlayan çizgilere izokronlar/eşhacim denir. İsochronal alanlarının dağılımı, zaman alan dağılımı, tüm taşkın hidrograf teorisi için belirli bir havza için sabit olarak kabul edilir.

Bu dağılımı hesaplamak için gerekli işlem veya ortalama bir yolculuk süresi veya ilk olarak akım ortalaması hızını kabulü gerekir. İzokronlar kanal veya ortalama yolculuk süresi geçecek su miktarının ortalama hızına uygun olarak havzanın haritası üzerinde çizilmiştir. Her bölgenin alan ve daha sonra bir planimetre kullanılarak belirlenen değerleri karşılık gelen zaman farkı karşılığı değerleri çizilmiştir (Şekil II.6.11 (b)).

Zaman alan dağıtımı için t birim süre, İzokronlar arasındaki saat farkı düzgün yağış için hidrografın bir göstergesidir. Her farklı bölgeler üzerinden yüzeysel akış miktarları farklı sonuçlanan yağışın pek çok dönemleri varsa:

Qtt = A1Vt + A2Vt–1 + A3Vt–2 + ... + AcVt–c+1 (6.30)

Burada Qt döneminde ortalama deşarj olup, t bitiş zamanı, A süre alanlı histogramın olduğu dönemindeki koordinasyonudur ve Vt aynı dönemde bölgesel yüzeysel akış olduğunu gösterir. Tutarlı birimleri sağlamaya özen gösterilmesi gerekir. Şekil II.6.11 (c) havzaya gelen düzgün yüzeysel akış üç periyodlu sonuçlanan hidrografın hesaplanmasını göstermektedir.

Sonuçta hidrografın su toplama havzasının gecikmeli özelliklerini yansıtır. Gerçek hidrografın kanal depolama etkilenebilir olduğuna göre, hidrografın denklem 6.30 hesaplanan depolama üzerinden yönlendirilir olmalıdır. Literatürde tanımlanan çeşitli yönlendirme tekniklerden birini kullanabilirsiniz. İki tür teknikler 6.3.5 açıklanmıştır. Genellikle gözlenen hidrograf teorisi simülasyonu için en iyi kombinasyonu elde etmek için çalışmada yanılma ile İzokronlar ve yönlendirme parametrelerini ayarlamak için avantajlı olduğu bulunmuştur.

İzokron yöntemi yağışların düzensiz dağıtımları durumunda, güvenilir bir şekilde yağış deseni çizmek için havzada yeterli sayıda yağışölçerler varken göz önüne alınmasına olanak sağlar. Bu birim hidrografın üzerinden bir avantaj daha önce açıklanmıştır.

Yeraltısuyu modelleme

Genel modelleme konuları

Yeryüzü kaynaklarının daha soyut hale gelmesi ve kirliliğin artan etkileri nedeniyle tükenmiş olması gibi nedenlerle yeraltı suyu insanlık için giderek önemli bir kaynak haline geliyor.

Yeraltısuyu kullanıcısı için gizlenmiş ve belirsiz varlık olması nedeniyle, korunması ve yönetimi maliyet bakımından pahalı ve bilimsel kanıt, bilgilerin yetersiliği ve konumunun belirsizliği nedeniyle miktarını ve karakterinin anlaşılması zordur. Sonuç oalarak, onun hacmi ve kalitesini ne ölçüde olduğunun değerlendirmesi amacıyla geliştirilmesi, yönetimi ve koruması, potansiyeli ve güvenilir hacmi ile kalitesini incelemek için temsili modellenmiş senaryolar geliştirilmesi için gereklidir. Bu bölümde, bilim ve bunların başlıca elemanlarının süreçlerini geliştirme, kontrol ile korunması ve pratik bir çerçevede dahilinde hidrojeolojik modellenmesinde kullanılan yöntemlerin bir özetini verir.

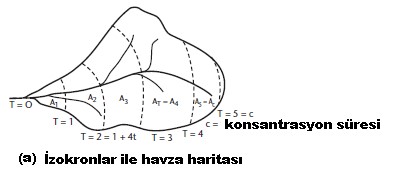
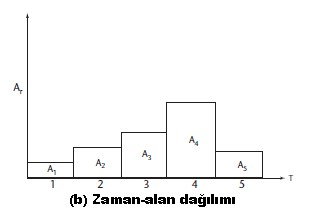
Şekil 11. İzokron yöntemi

Kavramsal bir model geliştirilmesi

Hidrojeolojik rejimi yeterince temsil edecek bir modelin kullanılarak çoğaltılması gereken çok sayıda özellikleri vardır. Bu modelin unsurlarını değerlendirmek için birçok temsilleri içermektedir (Bear, 1980, 1988).

Türü ve kavramsal model ayrıntısı ölçeği, üzerinde zaman ve kaynak miktarına bağlıdır - veri kullanılabilirliği, teknik uzmanlık, personel kaynakları, bilgisayar kolaylıkları - göreve atanan, karar verme süreci, mesleki risklerin yanı sıra yasal ve kanui çerçevenin kalitesi önemlidir.

Kavramsal modelleme sürekli ve dönemsel konumundadır; bu nedenle, temel bir kademeli yaklaşımın ayrıntılı bir aracı uygundur. Kavramsal modelde dahil varsayımlar aşağıda açıklanan sorunları arasında ilişki olmalıdır.

Matematiksel bir model geliştirilmesi

Modeli temel unsurları aşağıdaki bileşenleri içerir:

(a) Etki alanına bağlı olduğu yüzeylerin geometrisinin tanımı;

(b) Örneğin, akışkanların kütle, kimyasal türleri ve enerjisi kütle bileşenlerinin dengeleri ifade denklemleri;

(c) Sorunun ilgili değişken bileşenlerinin akılarıyla ilgili akı denklemleri;

(d) Belirli aşamaları ve kimyasal türlerin davranışı tanımlayan bünye denklemleri, basınç, sıcaklık ve çözünen konsantrasyonu yoğunluğu ve viskozite bağımlılığı dahil;

(e) Kaynaklar ve batma, genellikle bileşen miktarları fonksiyonları zorlama olarak anılacaktır.

Modelleme çalıştırılması açısından, ayarları aşağıdaki durumları kapsamaktadır:

(a) Sistemin ilk anda bilinen durumunu tanımlamak için bazı başlangıç koşulları;

(b) Kendi etki alanı dışında ortak sınırları boyunca vurgulanmıştır, onun çevre ile birlikte kabul edilen etkileşimini tanımlayan sınır koşulları.

Yeni bir sayısal model ve ilişkili kodu çalışır şekilde elde edilmektedir, matematiksel model çözümü için kullanılmaları gerekir ise sıkı bir doğrulama yönteminin, daha önceki kendini kanıtlamış uygulamaları aracılığıyla amaçlanan çalışma bakımından uygun olduğunu kontrol etmek için yapılmalıdır. Uygulama durumunda, karşılaştırmalı senaryoların farklı kodlarını kullanarak çalıştırmak gerekir.

Yeraltı suyu rejimi, jeolojik ve iklim koşulları tarafından kontrol edilmektedir ve çevresel şartların artan dengesi ile karşılanır iken sudan, kalkınma ihtiyaçlarını karşılamak için insanlar tarafından yararlanılmıştır. Varlığını saptamak için kapsamı ve kullanılabilir yeraltı su kaynaklarının değişkenliği, inceleme ile test etme mekanizmaları bir dizi şeklinde gerçekleştirilmiş olması gerekmektedir. Bunlar yerbilimleri kullanıcı tabanlı becerileri üzerine çiziler ile hidrometeoroloji, hidroloji, toprakbilimi, jeomorfoloji, petrolojisi, jeoloji ile su kimyası gibi çok geniş bir aralığı kapsamaktadır.

Yeraltısuyu dolaşımı, dünya su dolaşım sistemi ile sutaşıma oluşumları ve kanallar için iletim ve rezervuarlarının su depolama birimi olarak işlev gören yerkabuğunun hidrolojik çevrim olarak bilinen bir kısmını oluşturmaktadır. Su toprak yüzeyinden veya sonra bu mesafelerde değişen doğal akış, bitki ya da insan etkisiyle yüzeye dönene kadar yavaş bir seyahatle yüzey sularının kütlelerinde farklı formasyonlara giriyor. Yavaş akış oranları ile birlikte yeraltı depoları depolama kapasitesi, geniş ve kapsamlı bir şekilde dağıtılmış kaynakları sağlayabilir. Yeraltı suyu yüzey akışta mevcut olmayan seviyede düşük olduğunda dere akışlarını devam ettirmesinde yüzey suyu akım kanalları yardımları olarak ortaya çıkmaktadır. Benzer şekilde, su birçok bölgede kuyulardan pompalanır, yılın büyük bir döneminde birçok kurak alanlarda tek su kaynağıdır.

Suya doygun bölgesi içinde hidrolik durum tarafından belirlenen bir doğrultuda hareket eder ise toprak içerisinde su, yerçekimi etkisi altında doymamış bölgesi üzerinden aşağıya doğru hareket eder. Doğal beslenmenin başlıca kaynakları yağış, akımlar, göl ve rezervuarlar olarak bulunmaktadır. Yeraltı suyu deşarjı suyun yeraltında ortaya çıkıyor olmsından meydana gelir. En doğal akıntı yüzeylere, göller ile okyanuslar ve akış akarsuları gibi bir kaynak olarak görünür, yüzeysel su kütleleri halinde akmasıyla gerçekleşir. Toprak yüzeyine yakın yeraltı suyu zemin içerisinden ve bitki örtüsü gelen terleme yoluyla buharlaşma ile atmosfere doğrudan dönebilir. Kuyularda pompaj yeraltı suyunun büyük yapay bir akıntı oluşturmaktadır.

Yeraltı suyu, suyun hareketinin iletimine engel olduğunu geçirimsiz oluşumları olarak emilmesi ile birlikte doğal şartlarda gerçekleşecek su akışını kolaylaştıracak bir yapıya sahip akifer olarak bilinen geçirgen jeolojik oluşumlarda meydana gelir. Bir kayanın veya toprağın sağlam bir mineralli madde tarafından işgal olmadığını bir bölümü yeraltı suyu tarafından işgal edilmiş olabilir (Todd, 2005). Bu alanlardaki boşluklar, çatlaklar olarak bilinen gözenekleri veya gözenekli mekanların boyutu ve şekli, düzensizliği ve dağılımı tarafından belirlenir. Orijinal çatlaklarda ve jeolojik oluşumların kökenini yöneten süreçleri jeolojik olarak oluşturulan sedimanter ve volkanik kayaçların içinde bulunmaktadır. İkinci çatlaklarda kayaç oluşturulmuştur, sonra gelişen ve eklemlerde, kırıklar ve çözelti açıklıkları yer alıyor. Bir kayanın veya zemin gözenekliliği ve çatlaklarda bulunan bir ölçümüdür, kütlesinin toplam hacmi için buşluk oranına yüzdesi olarak ifade edilir. Eğer bir gözeneklilik ise:

a = 100w/V (6.31)

Burada w doldurmak için su hacminin olduğu veya doygunlaştırılacak gözenek alanının tümünü ve v kaya ya da toprak hacmi.

Gözeneklilik şekli ve bireysel parçacıkların boyut dağılımı ve sıkıştırma ile sementasyon derecesi düzenlenmesine bağlı olarak yüzde 50 ile yüzde 0 arasında olabilir.

Yeraltı suyu hareketi ve taşıma olayları temsil etmek için kullanılan modelleri vardır. Onlar şunlardır:

(a) Üzerinden bir sıvı tanıtılmıştır ve basınç ile baş enstrümantasyon tarafından izlenen bir ortamda oluşan ölçeklendirilmiş bir modeli kullanarak fiziksel bir gösterimi;

(b) İçinde tepe, akış ve iletkenlik gerilimi, akım ve direnç tarafından temsil edildiği bir elektrik gösterimi;

(c) Asıl işlemleri göstermek için algoritmalar kümesi kullanarak matematiksel gösterimi;

(d) Yüzeyaltı akımı ve taşıma modellemesini karakterize etmek için Stokastik bir analiz.

Uygulamada, şu anda en hidrojeolojik modelleme altına düştüğünde yukarıdaki (c) ve (d) kullanılır. İki ve üç fazlı akış koşulları gerçekleştiği yeraltı suyu kirliliği ile ilgili, taşınım olayları ile ilgili olarak matematiksel modellerin kullanımı temel temsil için karmaşık senaryoları ve analiz edilmiş olması nedeniyle kabul edilir.

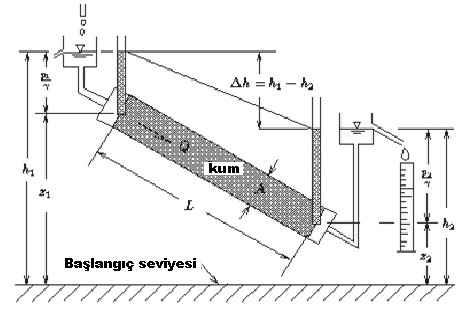
Doğal haliyle yeraltı sularının hareketi kurulan hidrolik ilkelere tabidir. Akiferlerin içeriye su akışı 1856 yılında Darcy tarafından çıkarılan bir yasa ile ifade edilebilen bir gözenekli ortam boyunca akım hızı yük kayıplarının ve tersine akım yolunun uzunluğuna orantılı olduğunu belirtiyor. Darcy yasası olarak genel hatlarıyla ifade edebilir:

Q = KA dh/dL (6.32)

Burada Q akım oranı, K geçirgenlik katsayısı (bazen hidrolik iletkenlik anılacaktır) ile dh / dL hidrolik eğim olduğunu. Bu ilişki Şekil II.6.12 gösterilmiştir.

Şekil 12. Darcy denemenin bir gösterimi

Bu şeklin isimlendirilmesi sayesinde, Darcy yasası aşağıdaki formu alır:

Burada, h (boyut: [L]) piyezometrik yükseklik olduğunu:

Burada z, hangi piyezometrik yükseklik bazı veriler seviyesinden kabul olunan noktasının yükseltidir, sırasıyla p ile ρ akışkanın basınç ile kütle yoğunluğu ve g yerçekimi ivmesi.

Şöyle hidrolik iletkenlik, K daha sonra ifade edilebilir:

Burada g yerçekimi ivmesi ile k (Boyut: [L2]) geçirgenliği veya gözenekli ortam içsel geçirgenliği konumundadır. Yalnızca yapılandırma alanının geçersiz alan özelliklerine tamamen bağlı bir katsayıdır.

Yeraltısuyu akımı ile hidrojeolojisi önemli bir yönü gözenekli ortam boyunca sıvıların akışını yönetmek ilkelere dayanmaktadır. Akışkanlar mekaniği, geniş bilgi gerektirir ama hidrojeoloji kısa bu çerçeve içinde yeterince tarif edemez. Ancak, yeraltı suyu akışı başlıca alt bölümleri akış, akış bölgesi ya da etki alanı sınırları ile orta ve akışkan özelliklerinin zaman bağımlılık boyutlu karakterine göre özetlenebilir.

Model işlem seçenekleri

Farklı seçenekler bir modeli tasarlarken seçilebilir:

(a) Modelin boyutluluğu (bir, iki veya üç boyutlu);

(b) Kararlı durum ya da zaman-davranış bağlı olarak;

(c) Sıvı fazların sayısı ve türleri ve alakalı kimyasal türleri dahil;

(d) Faz değişimi ve kimyasal türlerin bitişik aşamaları arasındaki alışverişi imkanı;

(e) Akışkanların akış rejimleri, örneğin laminer ya da laminer olmayanlar dahil;

(f) İzotermal olmayan koşullar ile sıvı ve katı özellikleri ile kimyasal-biyolojik süreçler üzerindeki etkisinin varlığı;

(g) İlgili durum değişkenlerini ve alanları veya birimleri gibi değişkenlerin ortalamalarının alınması gerekmektedir.

Doğadaki tüm yeraltı suyu akım derecesi belirli bir ölçüde üç boyutlu ama yeraltı suyu akım proplemlerinin çözümündeki zorluk derecesine bağlı olarak bir ölçüde akımın üç boyutlu olduğu üzerine bağlıdır. O simetrinin bir ölçüde mevcut olduğunu varsaymaktadır iki boyutlu bir problem cinsinden ifade edilebilir değilse doğal bir üç boyutlu akış problemini analiz etmek pratik olarak mümkün değildir. Sonuç olarak, birçok çözümleri iki boyutlu analiz sorunların olduğunu varsayımlara dayanır veya özel simetri özellikleri vardır.

Genel olarak, yeraltısuyu akımı niceliksel bir jeolojik oluşumu ile hız, basınç, yoğunluk, sıcaklık ve sızıntı suyu genişleme hızı gibi bir bilgiye dayalı değerlendirilir. Bu su özellikleri genellikle bilinmeyen değişkenlerdir, yer ve zaman içinde değişiklik gösterebilir. Bilinmeyen ya da bağımlı değişkenler sadece alan değişkenli fonksiyonlar ise, akım sabit olduğu kabul edilir; Eğer bilinmeyenler de zamanın fonksiyonları ise, akımın kararsız ya da zamana bağlı olduğu kabul edilir.

Yeraltı suyu dolu gözenekleri tarafından oluşturulan – akiferdeki – oluşan boşlukta yeraltı suyunun akım ortamının sınırlarına ve sınırlayıcı yüzey özelliklerine bağlıdır. Bu sınırlar akışının farklı durumları için zaman ve mekan içinde sabit ise akifer sınırlıdır. Ancak, eğer akış durumu ile değişen bir serbest yüzeye sahipse serbest konumundadır.

Akiferdeki yeraltısuyu akışının niteliği, özellikleri ve ortamının izotropikliği tarafından kontrol edilir. Çevrenin özellikleri herhangi bir noktada bu noktadan her yöne aynı olması durumunda yönbağımsız (izotropik) olarak kabul edilir; aksi takdirde o yönbağımlı (anizotropik) olarak kabul edilir. Doğası gereği, özellikleri veya izotropiklik ve koşulları veya anizotropide bir noktadan başka bir noktaya değişdiği takdirde ortam heterojen bir bileşim olarak kabul edilir, ortam ile doğası gereği özellikleri ile izotropik veya anizotropik koşullarda ortam boyunca sabit olduğu takdirde homojen bir yapının olduğu kabul edilir.

Başka bir alt bölümü, doymuş ve doymamış akış konumundadır. Ortamın boşlukları tamamıyla ana akışın faz sıvısı ile doldurulmuş olması durumunda akım doymuş konumundadır. Bu durumda değilse akım doymamıştır. Yukarıda geçirimsiz tabakaları örten bir durum olmadığında, suya doymuş ortamda yukarıda doymamış bir bölge olduğununda doymamışlık bölgesi derin sızma sonucu yeraltı suyu akışı her zaman doymuş olma konumundadır. Bu iki bölge arasındaki sınıra, su tablası veya yeraltı suyu tablası adı verilir. İkinci bölge kısmen hava ve su tarafından kısmen işgal edilmiş ve doymamış bölge veya havalandırma bölgesi adı verilir. Toprağın su bölgesi, bir ara bölgesi ile kılcal damar bölgesi olarak bilinen bir alt bölgesi olarak adlandırılan bir üst bölgesinden oluşur.

Küçük bir toprak nem eksikliğinde, bu uzun süreli yağış sonucu dışarıdan aşırı su girmesinin gerçekleşmesi ile oluşan doygunluk, toprağın su bölgesinde bulunmaktadır. Ana kök bölgesi yolu ile toprak yüzeyi bölgesine kadar uzanır; kalınlığı, toprağın türü ve bitki örtüsünün özelliğine bağlıdır.

Bir akifer üç temel hidrolik özelliklerinin depolandığı hacminin, bu veya doğal drenaj yoluyla da elde edilen verimi, pompalanır olduğunda ve geçirgenlik oranını yöneten bu hacmin kontrolleri, belirli bir verimi belirleyen geçirgenliğe sahip olduğunda su içerisinden akar.

Yeraltısuyu modellemesi yaklaşımları bir dizi literatürde yer alır. En sık görülen gözenekli fiziksel ortam akışıdır, titiz fizik kaynaklı yöntemlere dayanır. Bununla birlikte, kavramsal ve hatta kara kutu yöntemleride kullanılmaktadır.

Matematik, akış ve taşıma doymamış ve suya doygun geçirgen ortamda göreceli olarak oldukça karmaşıktır. Çeşitli konfigürasyonlarda, farklı varsayımlar ve basitleştirmeler için geliştirilmiş fiziksel bazlı denklemleriyle sınırlı olmak üzere sızıntılı ve sızıntısız çeşitli akiferler bulunmaktadır. Fiziksel temelli yaklaşımlarının klasik bir incelemesi Eagleson bulunabilir (1970). Ayrıca bkz: Maidment (1992).

Yeraltısuyu akış sürecinin kütle veya sürekliliği momentum korunumu ve bir durum denkleminin korunumunu ifade eden üç boyutlu doğrusal olmayan kısmi diferansiyel denklemler tarafından yönetilir. Sudaki önemsiz sıkıştırılabilirlik ve hiçbir kaynak ya da su giderleri ile geçirgen ortamda, izotermal kararsız bir laminer akış varsayımı altında, aşağıdaki diferansiyel denkleminin ile ifade edilebilir (Eagleson, 1970 bakınız):

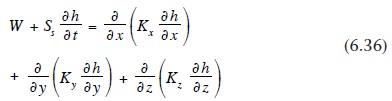
Burada h piyezometrik yükseklik, Kx, Ky, ve Kz hidrolik iletkenlik (Kx yönbağımsız ortamlar için Ky = Kz = k), W kaynakları ve su giderleri için kullanılan genel bir terimdir ve Ss özel depolamadır. Değişken olarak suya doygun akım formülasyonu olarak, doymamış hidrolik iletkenlik ve özgül nem kapasitesinin nem fonksiyonları bulunmaktadır.

Yeraltı suyu taşıma işlemlerini açıklayan bir eşitlik denklem 6.51 kullanılarak geliştirilebilir. Taşıma yatay akim-dağılım denkleminin ölçülü ve tepkisel durumlarda çözünen taşınması gibi yeraltısuyu akım yönleri kalitesini değişik şekillede simüle etmek için kullanılır.

Fiziksel yeraltısuyu akımı ve taşıma formu içinde bir çözüm genellikle sonlu fark veya sonlu elemanlar tarafından gerçekleştirilir, dağıtılmış yeraltısuyu modellerinin temel bir kısmi diferansiyel denklemleriyle elde edilir. Yeraltı su problemlerinin çözümü için bilgisayar yazılımına bir bakış, Anderson ve diğerleri (1992) tarafından yapılmıştır. HOMS bileşeni L20.2.04 dahil kodları arasında modüler sonlu farklılık yeraltı suyu akımı veya MODFLOW modeli, genellikle birçok uygulama dünya çapında kullanılmakta olan Amerika Birleşik Devletleri Jeolojik Araştırma Kurumu tarafından geliştirilen çok yönlü bir yazılım paketidir.

MODFLOW modeli, (McDonald ve Harbaugh, 1988) iki boyutlu olarak akım modellemesi kadar iyi üç boyutlu gözenekli bir ortamdaki yeraltısuyu akışını simüle eder. Modüler bir yapıya sahip olması nedeniyle modeli anlamayı ve değiştirmek gerektiğinde kolaylaştırmaktadır, sırasına göre program ve dokümantasyon için kullanılmıştır. Kodu elinizin altında bir sorun için seçilebilir paketleri veya modülleri bir seriden oluşur. Bu denklemler pompalama ve evapotranspirasyon, denklemlerin çözücüleri, dere, yeniden şarj için bilgi modüllerini içermektedir. MODFLOW bir uygulama alanında kararlı durum ve geçici yeraltısuyu akımı, sınırlı, sızıntılı ve serbest akifer ortamlarında yeraltısuyu akışını ve kaynak akış ve normal akış gibi bir de özel amaçlı akım problemleri şeklinde bir dizi içerir. Kuyular, nehirler, akarlar, evapotranspirasyon ve yeniden şarj ve simüle edilebilir baş-bağımlı kaynaklar olarak temsil edilen ya da modelin dışında baş-kullanıcı tarafından belirlenen koşullar içindeki bulunulan emiciliğidir. MODFLOW modeli böyle etkili akarsular ve kısmen göller için akıntı olarak yeraltı suyu ile yüzey suyu etkileşimleri arasındaki etkileşimi çalışmalarda kullanılabilir. Akifer hidrolik parametreleri, sınır koşulları, başlangıç koşulları ve stres modelin girişinde gereklidir. Metin dosyalarından veri, hazırlanmış kurallarla belirlenmiş düzen ve biçim ile girilir. Girdi verilerinin yapısı belirtilmiş grid yapısına uygun olması gerekir. Birincil modelinin çıktısı her bir model düğümününde ( node) başlangıcıdır. Buna ek olarak, bir su bütçesi hesaplanmış ve her bir modelin hücresi (gridi) üzerinden akım bir disk dosyasında saklanabilir. MODFLOW belki de dünyanın en yaygın olarak kullanılan yeraltısuyu modelidir.

MODFLOW paket deneyimli yeraltısuyu hidrologlar tarafından kullanılmak üzere tasarlanmıştır. Kullanıcının çabalarını azaltan yararlı ön-işlemciler ve son-işlemciler mevcuttur.

Planlama

Bir yeraltı modelleme proje üstlenmek için, ilk aşamada - ve çok önemli olan bir-işin amacını tanımlamaktır. Daha büyük projeler için, bir başlangıç kapsamı belirleme bakımından gereksinimleri tanımlamak ve projenin hedeflerini belirleyerek ve daha önceki çalışmaları ve kullanılabilir verilerin gözden geçirilmesi ve analizinin yapılması çalışmasını gerektirebilir. Yani, kapsam belirlemesi açısından projenin hedefleri ve yapılması gereken başlıca görevleri tanımlarken aynı zamanda çalışma için öngörülen ana hedefini tanımlamak gerekir.

Planlama aynı zamanda model yönetim kararlarının vermek için beklenen bilgi ve/veya mevcut bir izleme programı oluşturarak elde edilebilir durumda olması gereken verilerin türünün tanımlanmasını gerektirir. Ayrıca, uzmanlık dahil, vasıflı personel, izleme ekipmanı, arazi verileri ve model tespiti ve tanımlanabilir bütçe kısıtlamaları içerisinde bilgisayar sistemleri için mevcut kullanılabilir kaynakların belirlemesi projenin yürüyebilmesi için önemlidir. Bunu anlamak için model doğrulanması ve katsayılarının sayısal değerlerini belirlemek için gerekli verileri almak gerçekleşecek süreçleri açıklama ve tanımlama yeteneğini de içerir. Değerlendirme aynı zamanda model sonuçları yeterince kapsamlı sağlam ve ayrıntılı şekilde geleceğe yönelik incelemeleri karşılayacak şekilde emin olmak için dikkatli bir şekilde durumunuzla ilgili yerel yasal ve düzenlemeler çerçevesinde verilmelidir.

Bu proje rehberi, geçici çıkış incelemesi, görüş farklılıklarını gidermek ve modeli geliştirme sürecinin her aşamasında kabul edilebilirliği üzerinde bir anlaşmaya ulaşmak için ilgili paydaşları içermelidir, bu bakımdan bu durum bir yönetim ekibi oluşturmak için iyi bir uygulamadır.

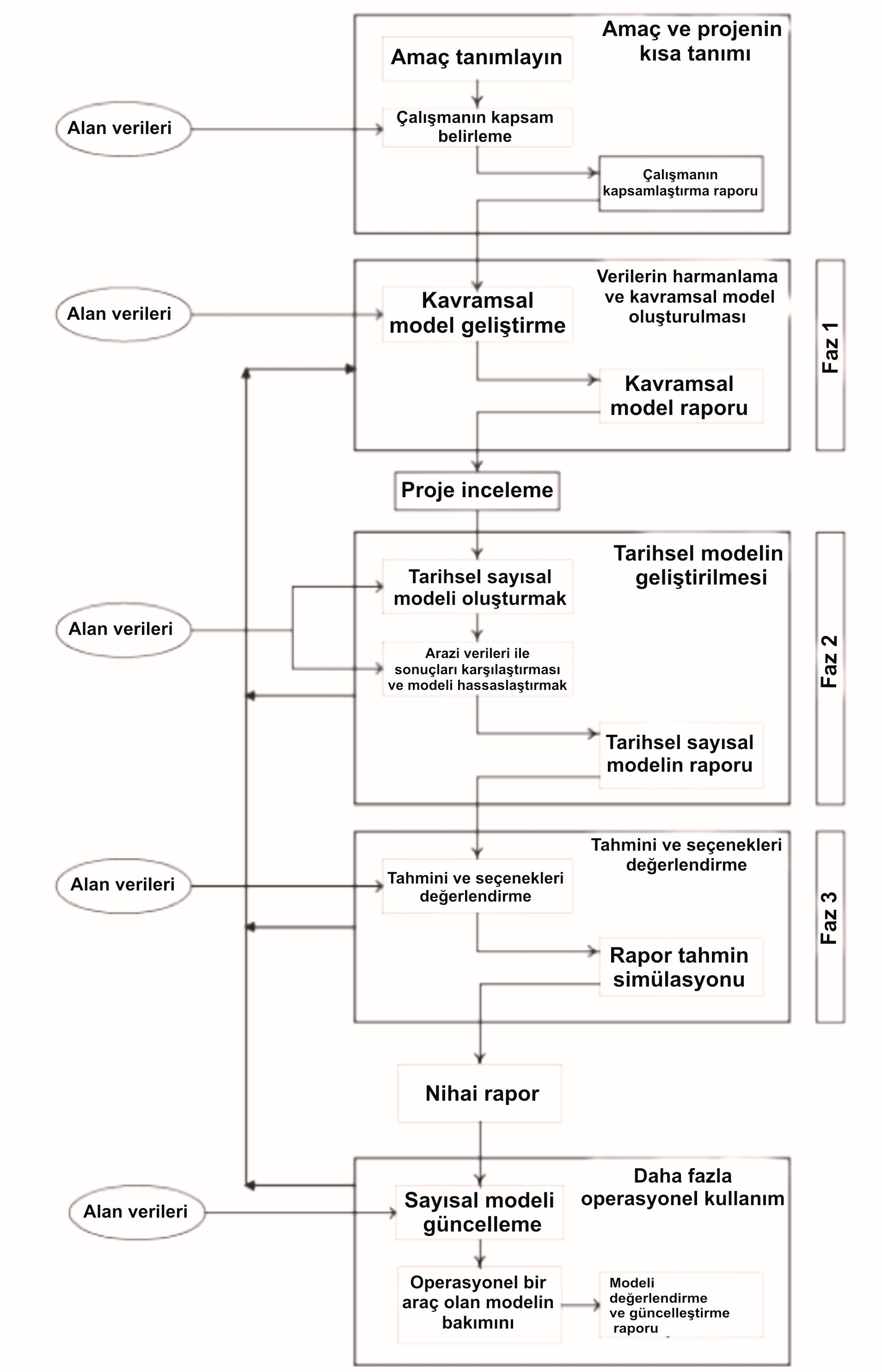
Modelleme projesinin hedefleri belirledikten sonra, aşamalı bir yaklaşımla genellikle yeraltı modelleme ile ilişkilendirilmiş belirsizlikler ve göreceli olarak yüksek maliyetleri ve uzun çalışma programı aralığı nedeniyle gereklidir. Bu sorunları kabul ederek, İngiltere ve Galler Çevre Ajansı (Çevre Ajansı, 2002) Şekil II.6.13 gösterilen yeraltısuyu modelleme sürecinde kabul edilmelidir ardışık aşamalarını ortaya koyan bir kılavuz üretti.

Yukarıda gösterilen yaklaşım kavramsal model ve daha sonra operasyonel veriler yardımıyla yapılabilir akıllı bir modeli ile biten tarihsel bir modeli kapsayan bir çalışmada ilerledikçe önemli bir karar destek sistemi oluşmaktadır. Bunların anlamı, hedeflere ulaşmak için seçeneklerin değerlendirilmesi, doğru seçenekleri elde etmek bir yanıt üretmek, sonuçlarını değerlendirmek, tercih edilen bir çözüm seçin ve sonuçları değerlendirmek için bir izleme sistemi oluşturmak gayesiyle tasarlanmıştır.

Kar-erime modelleri

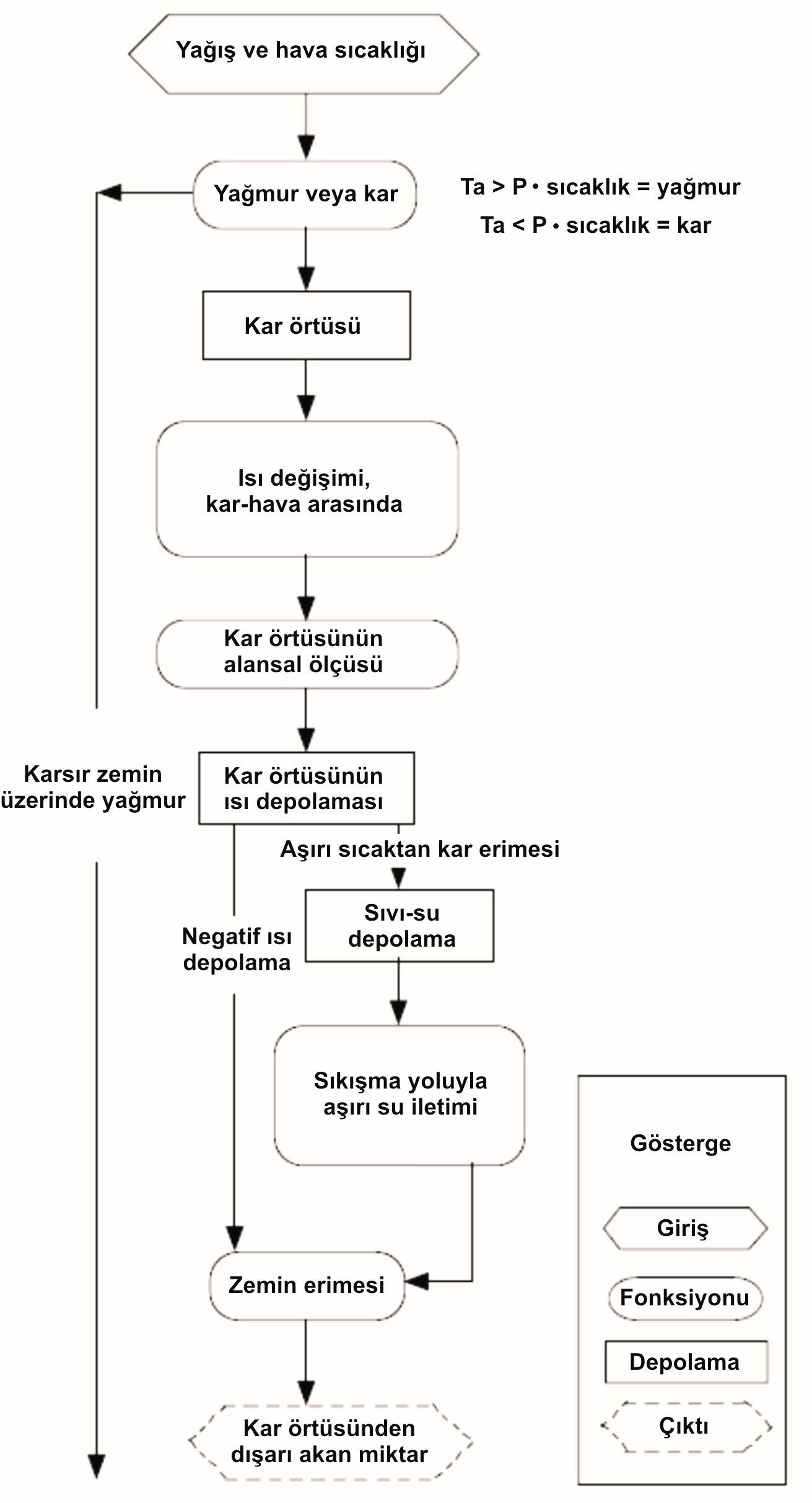
Kar erimesinden oluşan, kar örtüsündeki eriyen karın gecikmesi haricinde sızma ve yüzey akışı için su kaynağı açısından ilgisi yağış miktarına benzer. Bazı bölgelerde kar erimesinden oluşan su depoları, nehirler, göller ve akifer için başlıca katkı sağlayan durumundadır. Dağlık bölgelerde kar, kar erimesiyle genellikle toplam akımın yaklaşık yüzde 50 daha fazlasını oluşturarak yüzeysel akış önemli bir bileşeni haline gelir. Bazı dağ havzalarda, kar erimesinden yaklaşık olarak yüzde 95 üzerinde yüzeysel akışa neden olmaktadır.

Kar örtüsünün su eşdeğeri aşamalı değişiklikleri, olağan ölçümleri doğal gözlemsel ve örnekleme hataları sebebiyle kar erimesinden oluşan ölçümler tatmin edici boyutta değildir. Tahmin etme yerine, kar erimesinden oluşan gözlemler için iki ilave ve zorlayıcı nedenler mevcuttur. Bir akım, sadece sonuçta oluşan erime için beklemek yerine erimeye neden olan faktörleri tahmin etmenin tahmin için daha avanjlı olduğudur. Başka bir nedenle, tasarım ve planlama, özellikle fiziksel süreçlerin temelinde aşırı erime oranları tahmin edebilme ihtiyacıdır. Kar erimesi hidrolojik modellerde kısa bir incelemesi HOMS bileşenlerinin 6.1.6 gösterildiği gibi dahil edilmiştir.

Prensip olarak, kavramsal bir kar erimesinden oluşan yüzeysel akış modeli bir yağış miktarı-yüzeysel akış modeli ile kar birikmesi ve yüzeyden eritme için bir rutin birliktelik olduğudur. Ortak bir model yıl boyunca tahminde her türlü iklim koşullarında kullanılabilir. Kar erimesinden oluşan yüzeysel akış modellerde de bahar kar erimesinden oluşan dönem kullanımı için özel olarak geliştirilmiştir. Her durumda, bir kar örtüsünün erime enerji dengesi ile birlite yürütülmektedir. Enerjinin korunumu, kar sıcaklığındaki değişimin giren enerji akıları veya kar paketini terketmesiyle birlikte dengelenmiş olduğunu belirler. Bir kar örtüsünün içinde kütlenin korunumu aşağıdaki basit devamlılık denklemi ile ifade edilebilir:

Şekil 13. Yeraltısuyu modelleme süreci (Çevre Ajansı, 2002)

Çıkışlar süblimasyon (katı halden buharlaşma) ve yüzeysel akış ise girdilerin tüm birimleri ile birlikte su tipik olarak mm cinsinden ifade edilmiştir, yağış, yoğunlaşma ve dondurulmuş formlarda yüzey suyu şeklinde bulunmaktadır. Bir kar örtüsü için kütle değişimi, süblimasyon ile birikimi (Pomeroy ile Brun, 2001) ve zemin üzerindeki kar yağışları, gölgelik kesme etkisinde olabilir ve bunun yanında kar üflemesi aracılığıyla oluşabilir. Eengellenen karın bir kısmı da ağaçlarla kapalı alanda üflemeye maruz olabilir ve nihayetinde büyük bölümü süblimleşme olabilir kar örtüsü için bu bölüm kaybolur (kar gölgelik yakalanma konusunda daha fazla ayrıntı için, Hedström ve Pomeroy, 1998 bakınız).

Bu karmaşıklıklar nedeniyle, havza ölçeğinde kar fiziksel özellikleri ve ergiyik tanımlamak için kavramsal yöntemler geliştirilmiştir. Bunlar her ikisini de tanımlamak ve karla kaplı havzalar ve hidrolojik cevaplarını belirlemede pek çok operasyonel hidrolojik modelleme sistemlerinde kullanılan kar ortusu azalması eğrilerinin ve sıcaklık endeksi erime modellerini içerir.

Havza akış tahmini için indeks yöntemleri

Birçok orta ve uzun vadeli kar erimesinden oluşan akım tahmin modelleri istatistiksel indeksleme yöntemlerine dayanmaktadır. Dağlarındaki yağış ve kar örtüsü konusundaki kullanılabilir veri yokytur, bir kural olarak, hesaplama için zemin kar miktarı miktarına sağlar ve yalnızca bu değer indeks olarak sunulabilir. Bu nedenle, mevsimsel akış ve kar birikmesi indeksi arasındaki ilişkilerin istatistiksel bir doğası vardır. Amaç tahmin için uygun olsa da çoğu zaman su-denge analizleri için kullanılamaz.

Uzun vadeli tahminlerin başarısı kar-birikinti endeksi gerçek koşulları son derece iyi temsil etmesine çok bağlıdır. Yüzeysel akış üzerinde bazı etkiler ve dolayısıyla akış ve kar birikimi indeksi arasında korelasyon üzerinde olabilecek en az beş adet ek faktörler vardır:

(a) Önceki yeraltı depolaması;

(b) Son yapılan kar araştırma ve tahmini düzenlenmesi tarihleri arasında meydana gelen yağış miktarı;

(c) Kar erimesinden oluşan dönemde veya bunun için tahmin verildiği dönem boyunca yağış miktarı;

(d) Son araştırma ve tahminlerinin düzenlenmesi tarihleri arasında kar örtüsünün süblimleşme miktarı;

(e) Kar erimesinden oluşan dönemde veya bunun için tahmin verildiği dönemi boyunca kar örtüsünün süblimleşme miktarı.

Akiferlerden temel akım toplam yüzeysel akışın önemli bir oranını temsil eden ve önemli oranda değişmektedir, yıldan yıla göre değişen süreler için bu akarsu havzaları içinde korelasyon hassasiyeti önceki gelen yeraltı suyu koşulları göz önüne alınarak yükseltilebilir.

Yağış iki şekilde hesaba alınabilmektedir:

(a) Kar-birikimi ile indekslenmiş bir yağış indeksi kombine veya tek bir değişken olarak bu indekslerin toplamını kullanarak;

(b) Ek bir değişken olarak bir yağış indeksi kullanarak.

Daha sonraki yağış prosedürü geliştirilmesi sırasında akış ilişkisi dahil edilmelidir. Bu yağış etkileri istatistiksel kar erimesinden kaynaklanan tahmin ilişkilerinin dahil olmasını sağlar.

Finansal bütçeler izin verirse böylece kar araştırmaları kar birikimi eğilimleri elde edilebilir, kış aylarında dağlarda birçok defa yürütülmesi zorunludur. Nihai kar raporu araştırması genellikle ilkbahar kar erimesi başlangıcında hemen önce kar-birikimi döneminin sonunda yapılır. Kar-birikimi döneminin sonunda Kar-araştırma verileri kar birikim indeksi hesaplanması için kullanılır.

Çeşitli yüksekliklerde bulunan kar içerisinde kar su eşdeğeri ve yükseklik, w = f (z) arasında bir ilişki oluşturmak üzere verileri elde etmek için kullanılır. Farklı bir ilişki her yıl için elde edilmektedir. Gözlem verileri w = f (z) grafikler çizilmesi için yetersiz olduğunda, yüzeysel akış ve gözlem her noktasında kar su eşdeğeri arasında çoklu korelasyon kullanılabilir. Kar sahası verileri hala istatistiksel modellerde akımı tahmin etmek için giriş olarak kullanılabilir.

Çoğu durumda, suyun dağlık bölgelerden yüzeysel akış için kullanılabilen en iyi endeksi yağış ve kar-araştırma verilerinin bir kombinasyonundan geliştirilebilir. Bu istatistiksel yaklaşımlar tarafından gerçekleştirilebilir.

Kavramsal kar erimesinden oluşan yüzeysel akış modelleri

Havzadaki yüzeysel akış bir erime kalınlığındaki bir kar örtüsünün fiziğini temsil eden muhtemel algoritmaları bir dizi şeklinde kullanılarak tahmin edilebilir. Birçok yönden, erimiş olan karın muhtemel sızma algoritmaları kullanılarak toprağa matris olarak yağış miktarı ve sızmış olanla aynı kabul edilir. Kar erimesinden oluşan yüzeysel akış simülasyon modelleri genellikle kar erimesi modeli ve dönüştürme fonksiyonundan oluşmaktadır. Kar erime modeli yüzeysel akış ve dönüşüm modeli için geçerli olan kar örtüsünün sıvılaşmaya başlayarak suyu üretir, havza çıkışında yüzeysel akışa geçmesi için toprak yüzeyinde sıvı çıkışına dönüştüren bir algoritmadır (Donald ve diğerleri, 1995). Kar erimesi ve dönüşüm modelleri toplulaşatırılmış veya doğada dağıtılmış olabilir. Toplulaştırlmış modellerde bir havzanın fiziksel ve hidrolojik özelliklerini tanımlamak için parametre değerlerinin bir kümesini kullanın. Dağıtılmış modeller birbirinden bağımsız parametrelerini tali bölgelerin her biri için karşılık gelen bir dizi kullanarak her bir alt-bölge için alt alanlarda ve hesaplamada kar erimesinden oluşan yüzeysel akış olarak havzası içinde bölümlendirerek mekansal değişkenliğin hesaplanması girişiminde bulunuldu. Kar erimesinden modeller genel olarak (örneğin, Anderson, 1973, bkz) çok katmanlı bir kavramsal kar örtüsünün geçmek için, basit tek katmanlı bir kar örtüsünün arasında olabilir bir kar örtüsü temsili dahil olarak Brun ve diğerleri (1992) tarafından gösterilmiştir. Kar örtüsünün gösterimi suyun depolaması bakımından yeteneği nedeniyle kar erimesinden oluşan yüzeysel akış zamanlaması açısından etkileri vardır.

Birçok operasyonel kar erimesinden oluşan yüzeysel akış modelleri kar erimesinden meydana geldiğinde ve ne kadar kar erimesi zamanın belirli bir süre içinde meydana gelebileceğini belirlemek için bir sıcaklık endeksi veya bir derece-gün yöntemine dayanan bazı formunu kullanabilirsiniz. Kar birikim ve erime modelleri sıcaklık ve yağış miktarı kar-hava arayüz genelinde enerjinin alışverişinde tek başına indeks olarak kar örtüsü ve hava sıcaklık birikmesine kullanabilirsiniz. İkinci yönü genellikle kar örtüsü akan miktar endeksi olarak hava sıcaklığını kullanan derece-gün yöntemini kullanılarak modellenmiştir. Derece-gün yöntemi açıkça kar örtüsünün taşması kar erimesinin farklı nedenleri bu işlemler için diğer bir deyişle, bir ısı açığı ile saklama ve aktarımı sıvı suyun neden yeniden donma ve erimesinde hesaba katılmaz. Anderson (Anderson, 1973) tarafından geliştirilen modelin şeması Şekil II.6.14 ‘da gösterilmiştir. Kar araştırmaları veya nokta ölçümlerinden kar örtüsünün gerçek ölçümleri girdi olarak yalnızca sıcaklık ve yağış miktarı kullanımı kavramsal modellerinden mevsimsel hacim tahminlerini geliştirmek için bilgileri ek bir kaynak olarak kullanılabilir (Todini ve diğerleri, 1978).

Genişletilmiş akım modellemesi

Kavramsal modeller, yalnızca giriş verileri kullanılabilir dönem için yüzey akış kar erimesi benzetimini yapabilirsiniz. Gelecek için tahminler istatistiksel veya olasılıksal analizinden genişletilmiş veya sayısal hava tahmin modelleri kullanarak elde edilen yağış ve sıcaklık kullanılarak türetilmiştir tahmini değerlere göre yapılabilir. Geleceğe yönelik hava koşullarının etkileri dikkate alınmadığı takdirde mevsimsel yüzey akış dağılım paterni tatmin edici bir şekilde tahmin edilemez.

Endeks ve istatistiksel tahmin prosedürleri için, bu yağış ve sıcaklığın geçmiş kayıtlarına dayanarak sezonun geri kalanı için endekslerin kullanılmasıyla gerçekleştirilebilir. Kavramsal modeller için uzun yıllar klimatolojik veriler, genellikle 20 veya daha fazla, her yılın koşulları için varsayımsal yüzeysel akış dizileri geliştirmek için kullanılmalıdır. Olasılık dağılımları gelecekteki herhangi bir zamanda belirli bir süre için bu simülasyonları ve zirve akımı, hacim veya deşarj birim alandaki gibi belirli hidrolojik özellikleri için geliştirilmiş olabilir. (Twedt ve diğerleri, 1977). Bu önvarsayımlar tarihsel dizilerinin gelecek yıllarda neler olacağına temsilcisi olduğundan.

Şekil 14. Kar birikim ve buzun erimesi modeli akış şeması

Veri girişi

Kavramsal modellerin fiziksel tabanlı veya indeks türleri kullanılmak üzere giriş verileri ya yağış ölçümleri ve/veya kar örtüsünün su eşdeğeri ölçümleriyle olabilir. Fiziksel bazlı kavramsal modeller ile giriş verilerinin düzeltmeleri ortalama yağış ve/veya kar örtüsünün mümkün olduğu kadar temsili olması için yağış miktarı ölçümlerinin sistematik hatalar için yapılması (bkz: birim ben 3.3.6) gerekmektedir. Kar örtüsünün yüksek rakım bağımlıdır, dağlık olan bölgelerde, meteoroloji istasyonlarından gözlemler rüzgar, yerel eğim ve bakı gibi yerel maruz kalma olayından genellikle etkilenmektedir ve kar örtüsü koşullarını simüle etmek için kullanıldığında ortalama meteorolojik koşulları daha iyi temsil etmesi için ayarlanması gerekir. Uygulamada, kar örtüsü ve yağış miktarı ölçümleri birbirini tamamlıyor.

Kar örtüsünün alansal dağılımı genellikle en iyi şekilde ortalama derinliğin artmasıyla, kar örtüsünün özetlemeye en başında alansal kapsama alanını yüzde olarak azalma eğrileri kar örtüsünün tarafından açıklanmıştır. Havza genelinde kar örtüsünün azalması eğri ilişkileri şu anda kar örtüsünün erimesi olarak kar örtüsü dağılımını açıklamak için Ulusal Hava Servisi Nehir Tahmin Sistemi veya NWSRFS (Anderson, 1973) gibi toplu hidrolojik modelleri kullanılmaktadır. Bu ilişkileri elde etmek zor ve her belirli bir havza için kalibrasyonu gerektirir. Kar örtüsünün basit şekilde temsili, sabit derinliği ve eksiksiz alansal kapsama alanı olan düzgün kar örtüsü gösterimi vardır. Bilgilerin alansal dağılım dahilinde ve arazi birimleri arasındaki kar örtüsü toplam su eşdeğeri bir havzada mevcut kar örtüsü için makul tahminler yapabilmek amacıyla gereklidir. Daha sonra bir kara biriminin türü dahilinde karörtüsü ve alansal dağılımı konusundaki bilgi bir alansal dağılım eğrisi biçiminde özetlenmektedir. Bir alansal dağılım eğrisinin bir havza dahilinde belirli bir anda kar örtüsü durumunun bir özetidir. Yoğun örnekleme programlarının verilerini geliştirmek için gerekli olan alansal dağılım eğrileri şeklinde kar dağılım miktarını ayarlar.

Fiziksel karörtüsü dağıtım modeline pratik olmadığından, bu arazi örtüsü ve fizyografik değerlendirmeler temelinde istatistiksel veya deneysel dağılım ilişkilerinin geliştirilmesi sorununa mantıklı bir yaklaşımdır. Bu karörtüsü azalması eğrileri kullanıcı tarafından gerçekleştirilir. Rango ve arkadaşları, karla kaplı alan yüzdesini y ekseninde ve zamanı bir x ekseni üzerinde bir azalma eğrisi mevcuttur, bu yaklaşım havza kar erimesinden oluşan kavramsal temelli bir yaklaşım sağlar (Rango ve diğerleri, 1983).

Bir noktada kar-erimesi teorisi

Rasyonel bir yaklaşımla kar erimesi oranının ısı değişiminin anlamlı modları için hesaplamasını bir enerji bütçesine dayalı alarak tahmin etmek. Sıcaklık güneş radyasyonu, uzun dalga radyasyon, havadaki net ısı taşınımı, havadaki yoğunlaşma ile buharlaşma gizli ısısı, nispeten küçük miktarlarda yağmur ısısı ve altta yerden gelen zemin ısısını genellikle önemsiz miktarda emerek kara iletilir.

Enerji dengesi denklemi, kar erimesi için kullanılabilir enerji miktarını belirlemek için kullanılır, Qm direkt olarak kar biriminin küpü için kar erimesi miktarına dönüştürülebilir.

Qm = Qn + Qh + Qe + Qg + Qa – dSi /dt (6.38)

Buradaki ısı akıları (birim alan başına) sırasıyla şunlardır: Qn net uzun dalga radyasyon, Qh yüzey ve hava arasındaki sıcaklık farkı nedeniyle hissedilir ısı transferi, Qe su buharı değişiklik nedeniyle (yoğunlaşma veya süblimasyon veya buharlaşma tarafından kaldırılması ile ısının serbest kalması) gizli ısı akışı, Qg alttaki zeminden ısı iletimi, Qa ısı (yağmur) adveksiyon ve Si kar örtüsünün ısı depolaması.

Eriyen kar örtüsü, genellikle yüzde 2 ile yüzde 5 oranında kilo cinsinden sıvı su içerir, ancak iletim kapasitesini aşan kısa dönemler için zaman zaman erime oranları 10 yüzde olarak düzenlenmektedir. Böylece, kısa bir süre için, bir kar örtüsü tarafından oluşan serbest su toplamda mevcut gerçek meteorolojik koşullarda erimiş kar miktarını aşabilir. Pratik amaçlar için, önceden eritilmiş su bu sürümündeki dolaylı nedenle oluşan belirsizlikler ile yüklenmiş ve deneysel sabitlerinin içine dahil edilmiştir.

Emilen güneş radyasyonu enlem, mevsim, günün saatine, atmosferik koşullar, orman örtüsü, eğim, yüzey yönelimi ve kar yansımasına göre değişir. Enlem, mevsim, gün ve atmosferik koşulların zaman etkileri genellikle bu tür istasyonların seyrek ağı nedeniyle enterpolasyonla olması gerekir güneş enerjisi radyasyon gözlemleri dahil edilmiştir. Bu etkiler de bulutluluk derecesi, enlem ve yılın zamanı bir fonksiyonu olarak güneş enerji radyasyonu ifade formülleri veya diyagramlar vasıtasıyla günlük bazda toplamlar şeklinde hesaplanmış olabilir.

Güneş enerjisi radyasyon iletimi üzerinde orman örtüsünün etkisi önemlidir, deneysel alanlarda, bu iletim gölgelik yoğunluğu katsayısı ile ilgilidir deneysel bir faktör olarak ifade edilmiştir. Genellikle yönü ve eğimi ve orman örtüsünün dikliği belirli bir drenaj alanı için deneysel olarak elde edilen sabit faktörler tarafından temsil edilmektedir.

Karla kaplı bir yüzeyinden yansıtma aralıkları, iri taneli olan eski bir kar yaklaşık yüzde 40 ile yeni yağmış kar yaklaşık yüzde 90 aralığındadır, bununla birlikte bu normal rüzgardan savrulmuş organik veya toz mineralleri gibi koyu renki kalıntılarca ince bir tabaka tarafından mevsim sonlarında kaplanmıştır. Geç bahar aylarında orta enlemlerde, yansıtma özelliği düşük bir onmansızlaştırılmış kar örtüsünün yaygın olarak günlük su eşdeğeri 50 milimetre eritmek için yeterli güneş enerjisi radyasyonu absorbe eder.

Uzun dalga boyunda radyasyon değişimi, kar yüzeyi ile aşağı yönlü radyasyonun bulutları, ağaçlar ile atmosferden giden radyasyon arasındaki farktır. Yoğun alçak bulutlar veya ağır orman 0 °C daha sıcak örtü sayesinde, değişimi konusunda kar için bir kazanımdır. Bulutların veya orman örtüsü olmaması durumunda atmosferinden uzun dalga radyasyonun büyük ölçüde hava sıcaklığının bir fonksiyonu ile neredeyse her zaman kardan olan kaybı daha düşüktür. Uzun dalga boyunda radyasyon yönünden değişimi, su eriyik kaybı olarak günde 20 mm ye eşdeğer olması için genellikle günlük 20 mm eritebilir, bir ısı kazanç bakımından olduğunca fazla değişmektedir.

Duyarlı ısı konveksiyonel alışverişinde temel faktörleri havadaki sıcaklık gradyanının hemen üstünde kar ve yatay rüzgar hızı ile ifade edilen türbilans yoğunluğu şiddeti bulunmaktadır.

Yoğunlaşma bir ısı kaybı olarak temel faktörleri buhar basınç gradienti ve türbülans şiddeti, rüzgar hızı ile gösterilen biçimde bulunmaktadır. Türbülanslı değişim tarafından duyarlı ve gizli ısının birlikte değişim kaybına iki veya üç milimetrelik karşılık gelen günlük eritilebilirlik 100 mm fazla ısı kazancı eşdeğeri kadar değişebilir. Isı kaybı ile birlikte çok düşük hava sıcaklıklığı ve buhar basıncı ile buna kar yüzey sıcaklığı genellikle denk sıcaklıklığı ve buhar basıncı değişimleri için ısı kazancı 0°C ile sınırlı, kar sıcaklığı çok büyük olabilir çünkü potansiyel kazanç potansiyel kayıbı büyük ölçüde aşıyor. Böylece, değişimler azalır. Ilık yağmurdan gelen ısı artışı ile kar ve yağmur sıcaklık oluşmaktadır buz füzyonunudan itibaren (80 calg-l) gizli ısı hesaplanabilir, bu genellikle havanın ıslak termometre sıcaklığı olarak alınabilir. Hesaplamalar gösteriyor ki bir olağandışı şiddetli yağmur, 16 ° C sıcaklık ile en az 120 mm denk gelen yağmura karşılık olarak - kar erimesi olarak bir günde 25 mm kar erimesi üretimi için gereklidir.

Yeni oluşmuş bir kar örtüsü ile topraktan ısı iletimi hızı kısa bir süre için hızlı olabilir, ancak sıcaklığın normal jeolojik gradyan ve kararlı ısı gradyanı durumu oluştuktan sonra günlük kar erimesini miktarı yaklaşık olarak birer milimetre daha az üretilecek şeklinde kurulmuştur.

Isı değişimi çeşitli modlar arası daha once belirtilen oranlar kar erimesinin katkısı değildir. Örneğin, en çok çalkantılı değişim koşulları en fazla güneş radyasyonu ile değil de fırtınalı hava sırasında oluşacaktır. Çok sayıda denklemler, gözlemlenebilir unsurları açısından ısı değişimini ifade eden modlarını yayınlanmıştır. Daha fazla bilgi için bakınız WMO-No. 749, Operasyonel Hidroloji Rapor No 35 –Kar örtüsü Ölçümleri ve Yağış ve Toprak Neminin Alansal Değerlendirmesi (WMO, 1992) ve WMO-No. 646, Operasyonel Hidroloji Rapor No 23 (WMO, 1986) - Kar Erimesi Akış Modelleri ve Döngülü Karşılaştırılma.

Önemli bir boyutta karmaşık/heterojen drenaj alanı üzerinde rasyonel bir kar erimesi fonksiyonunun entegrasyonu en iyi şekilde pratik olarak yapma konusunda ayrıntılı cihazlar olmadan son derece güçtür ve boşunadır. Miktar veya eritebilir oranının tahmini ısı bütçe hesabına ilaveten su bütçesi hesabını temel alır. Yağmurun yokluğunda, radyasyonal değişimi ve nispeten önemli kar yansıması ve ormanlardan kaynaklanan gölgelik yoğunluğu dolayısıyla etkileri önemlidir; Ancak bunlar nadiren ölçülmektedir. Yoğun yağış dönemlerinde, kar erime miktarı ve oranı hesabında ve yağmurun etkilerini hesaplamalarda hata miktarı daha büyük olabilir. Önemli çalkantılı eşliğinde fırtınalar sırasında karıştırma ve koyu ve alçak bulutlar, nispeten daha az kısa dalga dalga boylu güneş ışınımı ve ısısal radyasyonu, konveksiyon ve yoğunlaşma ısısının önemli kaynaklarıdır. Bu kadar kar erimesi ve çok küçük deneysel değerlendirmeler ile birlikte teori alanında büyük oranda yağmur sırasında kar erimesi sorusuna bırakmıştır, yağmurun katkısının ayrıştırılması önemli bir sorundur (ABD Kolordusu Mühendisleri, 1960). Verilen bir enlem ve yılın hangi zamanında için günlük güneş ışınımı yerel bulutluluk tarafından etkilenir, bununla bereber subjektif olarak ve çok seyrek görülür -nadiren olan ışınımsal iletkenlik ile ilgilidir. Ayrıca, kar ya da aktif bir katkıda bulunan alanın belirlenmesinde problem vardır.

Aktif ya da katkıda bulunan kar erimesi alan üzerinden ya da toprak üzerinde aştığında erime alanı olarak tanımlanabilir. Ancak tanımlanan bu alan, günlük olarak değişir. Günlük döngüsü gece donma içeriyorsa, bazı hesap ilgili ısı ve nem depolama alanı alınmalıdır. Erken erime döneminde, bir miktar ısı ve 0 ° C kar sıcaklığı yükseltmek için kar örtüsünün su tutma kapasitesini karşılamak için yeterli kar eritmek için gereklidir. Bu ısı, kar örtüsü eritmek için gerekli toplam ısı açısından nispeten azdır.

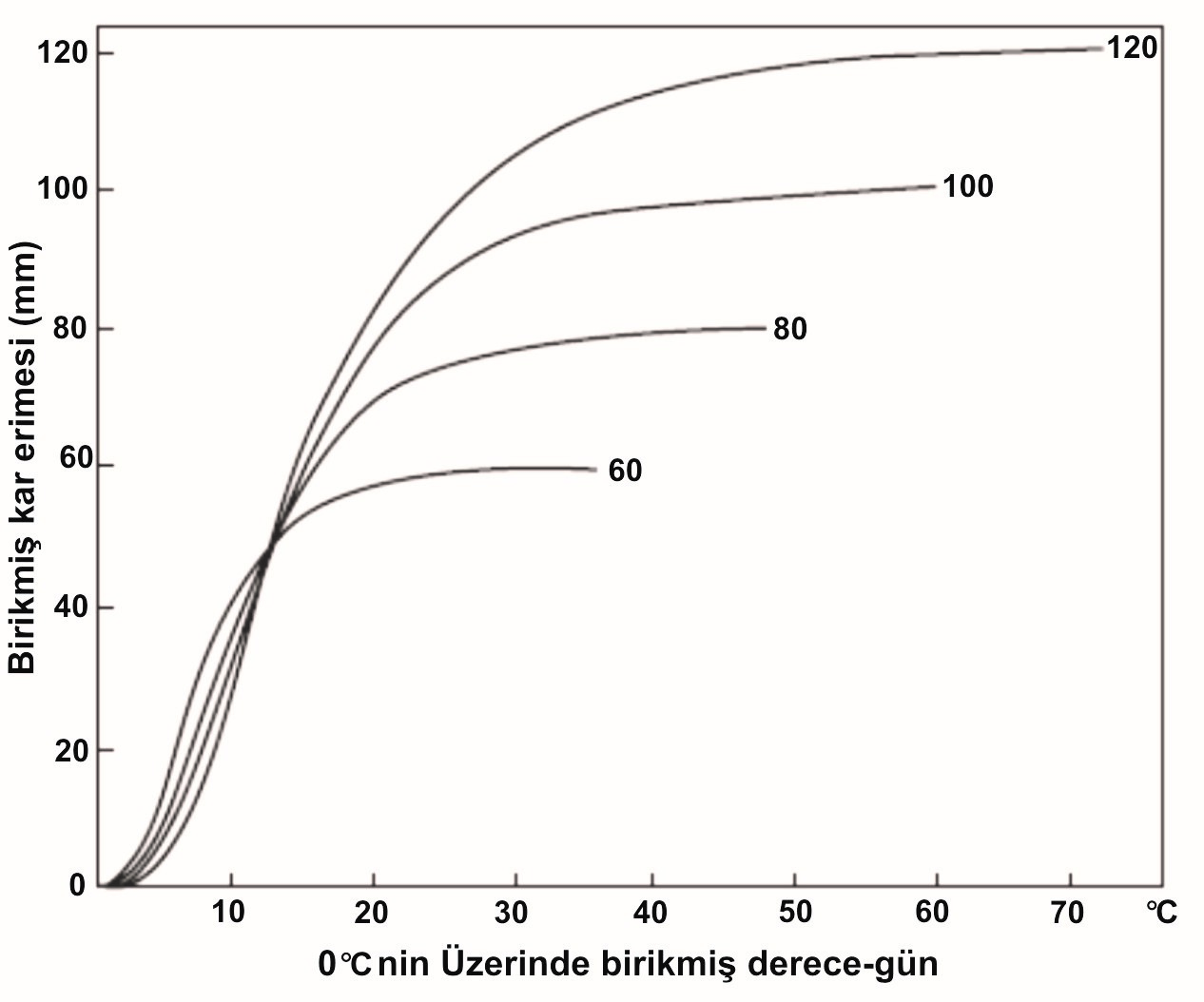
Havza genelinde kar erime tahmin etmek için en sık uygulanan yöntem derece-gün faktörlerini kullanmaktır. Sıcaklık verileri ve genelde mevcut bir drenaj alanda üzerinden sıcaklığın değişimi, genellikle türetmeniz ve derece-gün işlevleri uygulamak için belirlenebilir. Derece-gün yöntemi için mantığı iki yönlüdür. Öncelikle kar yakınında hava sıcaklığında büyük ölçüde kar erimesine ısı değişimi aynı modlarının fiziksel bir bütünleşmesidir. İkinci olarak, her tarz ısı değişimi hava sıcaklığı dışında olağandışı rüzgarlar esnasında hava ile ilişkili olabilir. Örneğin, asgari günlük hava sıcaklığı son derece yoğunlaşma erimesi için buhar basınç gradyanı belirleyen çiğ noktası sıcaklığı ile ilişkilidir. Günlük maksimum sıcaklığı veya sıcaklık aralığında güneş ışınlarının bir endekstir. Her zamanki kapsam alanında, uzun dalga ışınımı hava sıcaklığın doğrusal bir fonksiyonu olarak ifade edilebilir.

Çalışmaları çeşitli ağırlıklar maksimum ve minimum günlük sıcaklık vermek ve 0 °C. dışında derece-gün esasında kullanımı için yapılmıştır. Çabaları da daha küçük zaman birimi halinde derecede saatlik faktörlerin kullanmak için günü bölümlendirmek gayesiyle yapılmaktadır. Ancak, ısı değişimi ile kar erimesi ve günlük döngüsü, normal derece-gün temelinde günlük kar erimesi için günlük mantıksal ve uygun bir birimi haline getirir, genel olarak günlük maksimum ve minimum hava sıcaklıkları ortalaması 0 °C olarak alınmaktadır. Kuzey Amerika'nın orta enlemlerinde birkaç dağlık bölgeleri için kar erimesi noktadan derece-gün faktörleri ve eriyik milimetrelik olarak, Tablo II.6.3 de ortalama olarak olmuştur, 0 °C'nin üstünde temel günlük maksimum ve minimum sıcaklığın ortalaması Tablo II.6.3 de ortalama olarak kabul edilmiştir. Bireysel değerleri yaygın olarak bu ortalamalardan çok farklıdır.

Benzer derece–gün faktörler için eski Sovyet Sosyalist Cumhuriyetler Birliğinde orta enlemlerdeki ovalar için tablo II.6.4’de verilmiştir.

Sığ bir kar örtüsü, depolama ve örtü içinden geçen su erittiği gecikme ile depolama ve gecikmeli toprakta mantonun ve belirsizliklerin kendisi kar erimesi miktarı ile karşılaştırıldığında, genel olarak önemsiz bulunmaktadır. Bir kar örtüsü akmasına sıvı su için gereken süre yaklaşık bir saat, artı derinliği her 50 cm için bir saattir.

Erime hızı ve dağıtımı ve bir erime dönemi boyunca karla kaplı alanın büyüklüğü azalan alansal varyasyonları kendi topografyası ve bitki örtüsünün dağılımı gibi havza alanının oldukça kalıcı özellikleri ile ilgilidir. Dolayısıyla, bir havza üzerinde erime hızı bir erime dönemi boyunca alan ve kar durumuna katkıda bulunmak için oldukça tutarlı bir eğilimi yansıtmaktadır. Bu eğilim, Şekil II.6.15 olanlar gibi deneysel olarak tanımlanmış S-biçiminde eğrilerinin şeklini etkiler. Karın alansal dağılımı nedeniyle ve yerel erime oranları karın bir kısmını dinlenme öncesinde erimeye başlar. Böylece, birim alan başına ortalama eritebilir oranı erken erime döneminde yetersiz ve alanda katkısı daha fazla artar. Erime döneminin sonuna doğru, Şekil II.6.15 eğrileri yamaçlarında kar erimesinden katkısının azalması alanı nedeniyle azalır. Erime koşullar büyük bir katkıda bulunan alan üzerine kurulu olduktan sonra eğrilerinin en keskin bölümlerini meydana gelir. Kar başlangıç miktarları oranlarının erimesinin orantısal olarak daha fazla olması, büyük ölçüde katkıda bulunan alanın daha büyük olmasından meydana gelir. Şekil II.6.15 ve eğrilerinin en keskin bölümlerini Tablolar II.6.3 ve II.6.4 değerlerine karşılık gelen bir eğimi vardır.

Tablo 3. Kuzey Amerika'da dağlık bölgeler için derece-gün faktörleri (mm ° C-1)

Ay	Orta Dercede Ormanlık	Kısmen Seviyede Ormanlık	Ormanlık Olmayan
Nisan	2	3	4
Mayıs	3	4	6
Haziran	4	6	7

Tablo 4. Eski Sovyet Sosyalist Cumhuriyetler Birliği’nin ova bölgeleri için derece-gün faktörleri

Alan	Derece-Gün Faktörleri (mm °C-1)
Ormayanlık olmayan alanlar	5
Sert ve seyrek iğne yapraklılar ve ortalama yoğunluk	3-4
Kozalaklı ağaçların ortalama yoğunluğu ve yoğun karışık orman	1.7-1.8
Yoğun iğne yapraklı ağaçlar	1.4-1.5

Şekil 15. Başlangıçtaki su eşdeğerinin farklı değerleri için bir havza için tipik derece-gün olarak kar erimesinden oluşan ilişki

Kar örtüsü kaybından buharlaşma erime kısa dönemlerde ihmal edilecek küçüklükte olduğunu ve daha fazla kar yüzeyinde yoğunlaşma tarafından dengelidir. Bir kar örtüsü üzerinde yoğunlaşma denklemleri de kardan buharlaşma tahmin etmek için kullanılabilir. Kar ya da buz yüzeyinden buharlaşma ölçümü genellikle zor ve muhtemelen yaklaşık buharlaşma hesabı kuramsal olarak doğrudur. Bu kış dönemlerinde tipik kar yüzeyinden buharlaşma sıfır olduğu kadar ayda 20 mm arasında değişen oranlarda oluştuğu tahmin edilmektedir. Erime dönemlerinde, yoğunlaşma eğilimi hakim ve büyük olasılıkla olduğunca fazla günlük 10 mm yoğunlaşma itibariyle sıfıra kadar uzanan oranlarda gerçekleşir.

Dağlık bölgelerde, yerde kar büyük miktarda birikebilir, buradaki sezon erime koşullar Şekil II.6.15 de olanlar gibi eğrilerin güvenilirliği sınırlıdır, yükseklik geniş bir ürün yelpazesi ile büyük ölçüde değişir ve birkaç ayı kapsayabilir. Buharlaşma uzun sıcak dönemlerde önemli olabilir. Erime sezonunda başarılı hava veya diğer anketler ve değişen karla kaplı alanı göstermek meteorolojik gözlemlerin yükselmesi ile erime hızı değişimini ifade etmek için yorumlanır. Kar erimesinden olan katkısı yükselme bölgeleri tarafından tespit edilmelidir. Buna ek olarak, daha fazla değerlendirme kar örtüsünün derinlemesine dağ ile birlikte örtüsü içinde erimiş kar tutması verilmelidir.

Ortalama derece-gün faktörü daha yüksek olarak olağandışı yüksek rüzgar hızı veya nem meydana geldiğinde kullanılmalıdır.

Kar erimesinden giriş oranları Tahmini

Alçak havzalardaki toplam kar erimesinden oluşan yüzeysel akışı belirlemek için su dengesi çalışmaları kabul edilebilir. Bunlardan, beklenen toplam kar erimesinden oluşan yüzeysel akış kar erimesinden oluşan dönemin başlangıcında tahmin edilebilir. Ancak, günlük kar erimesinden oluşan giriş değerleri genellikle hidrograf hesaplamaları için gereklidir. Aşağıdaki faktörler bu değerlerin tahmin edilmesinde dikkate alınmalıdır:

(a) Kar örtüsüne ısı girişi;

(b) Kar örtüsünün su tutma kapasitesi;

(c) Karla kaplı alanı;

(d) Havzanın su tutma kapasitesi.

Muhtemel maksimum yağış ve kar erimesi

Yağış miktarı yerine, yüksek enlemlerde çok büyük havzalarda yağışdan oluşan kar erimesinden ziyade olası maksimum taşkın durumunda birincil nedeni olabilir. Sel-yüzeysel akış hacmi ve zamansal dağılımı daha sonra bir şekilde sıcaklık, rüzgar, çiğ noktası sıcaklığı ve güneşlenme tahmini maksimum değerlerininin fırtına yağış maksimizasyonuna benzer şekilde kaynaklanan kar erimesinden oluşan tahminine dayanmaktadır.

Düşük enlemlerde daha yaygın bir durum yağışlardan oluşan kar erimesinden maksimum hidrograf için bir artış ekleyerek olası maksimum taşkın üretiminde başlıca faktör olmasına yöneliktir. Kar erimesi, fırtınanın en üst düzeyde eşlik eden tahmin sinoptik koşulları ile birlikte uyumlu, daha sonra en üst düzeyde yağışların derinliği eklenir.

Bazı havzalar için, sadece ayrıntılı bir analiz olası maksimum taşkın kar erimesi ile birlikte veya ancak daha fazla yoğun olabilir mantıklı kar erimesi ile birlikte gerçekleşmesi beklentisi mümkün değildir bir yaz yağışı kombine bir serin mevsim yağmur fırtınası sonucu olup olmadığını ortaya çıkaracaktır.

Muhtemel maksimum kar birikmesi

Olası maksimum taşkın için kar erimesi katkısı, erime katkılarını.n maksimum hızı ve erime için kullanılabilir kar örtüsü su eşdeğerine bağlıdır. Bir kar örtüsünün su eşdeğeri, erime sonucunda ortaya çıkacaktır ve karın derinliği gibi yoğunluğuna bağlıdır. Çeşitli yöntemler olası maksimum kar birikmesi tahmin etmek için kullanılmıştır; aşağıdaki gibi en çok kullanılan üç tanesi şunlardır:

(e) Kısmi sezon yöntemi - Gözlemlerin frekansına göre her ay ya da iki hafta sürelere göre en yüksek görülen kar birikimleri, yapay bir yıl için çok yüksek kar vermek amacıyla her gözlem geçtiği yıl bakımında bağımsız olarak birleştirilir. Uygun kayıtların mevcut olması halinde yöntemi, bir hafta ya da dört günlük süre gibi daha kısa zaman aralıklarında uygulanabilmektedir;

(f) Kar fırtınası maksimizasyonu – Hangi bir kar fırtınasının, kar fırtınası gerçek nem içeriğiyle gerçekleşir, yıllık zamanda proje alanındaki maksimum atmosferik nem oranı belirlenir. Kar fırtınası tarafından üretilmiş gözlenen kar yağışı kar fırtınası için en üst düzeyde kar yağışını vermek için bu oran ile çarpılır. Nem içeriğinin maksimizasyonu yağmur değil, kar üretecek bir değer ile sınırlı olmalıdır;

(g) İstatistiksel yöntemler – Yağış ve kar-derinliği kayıtları frekans analizleri çeşitli geri dönüş süre değerlerini belirlemek için yapılmaktadır. Verilerin analizleri üç şekilde yapılmaktadır: istasyonu yağış derinliği, havza kar yağışı derinliği ve zemin üzerinde kar su eşdeğeri.

Kar erimesi tahmini

Eğim, bakı, orman örtüsü ve kar örtüsünün derinliği farklılıklardan kaynaklanan en fazla havza üzerinde kar erimesi karmaşık mekansal ve zamansal değişkenliği nedeniyle, derece-gün yöntemi genellikle havza üzerinde kar erimesi tahmin edilmesi sorununa pratik bir çözüm olarak benimsenmiştir. Maksimum derece-gün koşulları ve hava sıcaklığı kayıtlarındaki proje havza ya da komşu bir alan için tahmin edilebilir ve olası en büyük sel akışı konusunda bir tahmin sağlamak için olası en yüksek kar birikimini tahmin etmek için uygulanabilir.

Muhtemel azami koşulları için, hava sıcaklığı ve rüzgar fırtınası hızı üreten, muhtemel azami yağış miktarı beraberindeki varsayılan sinoptik koşulları ile birlikte tutarlı hale getirilmiştir. Aynı zamanda en uygun kar örtüsü mevcut olduğu kabul edilir. Bu durumda en uygunu, aşağıdakiler gibi olduğu anlamına gelir:

(a) Kar örtüsünü fırtına esnasında tümüyle eritmek için sadece yeterli bir su eşdeğeri vardır;

(b) Kar örtüsü erimesinden oluşan ve sıvı suyu maksimum miktarda içerir;

(c) Kar örtüsünün su eşdeğeri, artış yüksekliği ile birlikte kar örtüsü su eşdeğeri artan olağan durumu farklıysa, en fazla olduğu bir üst seviye olmak üzere dağıtılır.

Kısa-dönemli kar erimesinden oluşan akış

Bir ova bölgesinde, nerede akış adımlarıyla ve nispeten küçük olduğundan erime süresi kısa bir yüzeysel akış, yukarıda bahsettiğim yöntemler ile elde edilen kar erimesinden oluşan bir yağış-akış ilişkisi tahmini birleşimiyle tahmin edilebilir konumundadır (bakınız: 6.3.2). Kar örtüsü veya soğuk havalarda erime dönemine göre öncül buharlaşma kayıplarını engeller çünkü, yüksek oranda yüzeysel akış yansıtır bir şekilde ilişki kullanılması için gerekli olabilir. Dağ havzaları olarak, nerede kar örtüleri hakim ve erime sezonu birkaç ay süren ikinci tur gelen kısa yağmur fırtınaları tahmininde kullanılan yöntemler mutlaka geçerli değildir. Kar örtüleri ve geçerli erime mevsimi yöntemleri sıklıkla zorunlu olarak geçerli değildir, kısa süreli yağmur fırtınası akanlarını tahmin etmek için kullanılabilir ve birkaç ay sürer. Yüzeysel akış belirli bir günde meydana gelen erimeden genellikle diğer pek çok günlük erime aralıklarla örtüşen uzun bir süreye yayılır. Ayrıca, yağış miktarı bir süre içinde ihmal edilebilir evapotranspirasyon kayıpları, uzun bir erime sezonu boyunca önem kazanmaktadır. Günden güne kar erimesinden oluşan akarları tahmin etmenin bir yolu, yüzeysel akışın mevsimsel hacminin hesaplanabilmesi ve daha sonra gözlemlenen veya tahmin edilen yerel günlük erime oranları uyarınca (6.3.4.6 ve 6.3.4.7) dağıtmanız için ilk olarak, havza-depolama özellikleri ile katkı sağlayan alanda mevsimlik bitki su tüketimidir. Havza depolama ve gecikmesi tarihsel havza verilerinden deneysel olarak belirlenen sabitler ile rezervuarlarının benzer bir sistemi olsa da yönlendirme yapılarak ayarlanamaz. Havzada kar erimesinden oluşan ve günlük aralıklarla depolama birimi tarafından sönümlü olmadığı kadar küçük olması halinde, altı saatlik emdirilmiş değil,- bunun yerine günlük erime artışları ya da kullanılması gereken bir karakteristik günlük dağılım yönlendirme yöntemi girmiş olabilir.

Uzaktan algılama kullanarak kar erimesi yüzeysel akış analizi

Kar erimesinden oluşan yüzeysel akış prosedürlerinde iki farklı yol izlemiştir: deneysel bir yaklaşım ve belirleyici modelleme yaklaşımı. Bir yaklaşımın seçimi kar örtüsünün ölçülmesi için her iki verinin kullanılabilirliği ve çıkışının gerekli detayların kapsamasına bağlıdır. Kar erimesinden oluşan yüzeysel akışın tahminlerini doğru yapmak için, hidrolojistlerin aşağıdaki açıdan kar erimesini ölçülmeleri gerekmektedir: karın alansal büyüklüğü, S; kar su eşdeğeri, SWE; ve koşul veya derinlik, yoğunluk, tane büyüklüğü ve sıvı suyun varlığı gibi kar özellikleri (Engman ve Gurney, 1991). Kademeli olarak azalan alansal kapsamı mevsimsel kar örtüsünün karakteristik bir özelliğidir. Tarihsel veriler veya belirleyici yaklaşıma dayalı deneysel bir yaklaşım olduğuna bakılmaksızın, kar erimesinden oluşan yüzeysel akış günden-günümüze simülasyonlarını yapmak için kullanılan yaklaşım ne olursa olsun başlangıçtaki birikimi bilmeden havzadaki günlük karla örtülü alanı bilmek kar su eşdeğeri açısından yeterli olacaktır (WMO, 1994).

Birçok havzalar için, yüzeysel akış ve kar örtüsü alanı arasında oldukça iyi bir ilişki vardır (Engman ve Gurney, 1991). Operasyonel yüzeysel akış tahminleri için ancak, su eşdeğeri de tespit edilmelidir (WMO, 1994). Uzaktan algılama amacıyla kar erimesinden oluşan yüzeysel akışı tahmin etmek, kar verilerini elde etmek için yeni ve değerli bir bir araç sunmaktadır (Engman ve Gurney, 1991). Ostrem ve diğerleri (1991) kalan kar ölçümü ve Norveç yüksek dağlık havzalarında bir dizi için karşılık gelen kar erimesinden oluşan yüzeysel akış hacmi tahmin etmek için Ulusal Okyanus ve Atmosfer Kurumu (NOAA) ve televizyon kızılötesi gözlem uydusu (TIROS) verilerini kullanarak bir yöntem geliştirdi. Birçok büyük hidroelektrik şirketlerinin kendi hidroelektrik üretiminin planlanması için NOAA AVHRR verileri girdi olarak kullanarak, bir işletme bazında oldukça yüksek çözünürlüklü bir radyometre ile ileri düzeyde, kapsamlı kar örtüsü haritalarını kullanır (1991 Andersen).

Uygun dalga boyunda bantlar kullanılarak uzaktan algılama teknikleri tane büyüklüğü, albedo, tabakalanma, yüzey sıcaklığı ve kar örtüsünün sıcaklığı gibi belirli bir dereceye kadar kar örtüsünün özelliklerinin tahminini sağlar. Böylece, kar örtüsünün ve olgunlaşmış bir durumu olarak bilinen alt katmanları için yüzeysel su eriyiğinin nihayetinde kar örtüsünün üste yüzeysel akış üretimi bakımından iletmeye hazır olduğu zaman için iyi bir tahmine olanak sağlar (Rango, 1993). Uzaktan algılama kullanarak kar erimesinden oluşan yüzeysel akış tahmini konusunda ilk deneysel yaklaşım Rango ve diğerleri (1977) tarafından geliştirilmiştir; onlar Himalayalar'daki İndus ve Kabil Nehirler için geliştirilen deneye dayalı regresyon modellerinde uydudan gözlenen karörtüsü verilerini kullandı. Martinec ve Rango (1987) ve Rango ve Van Katwijk (1990) daha sonra uzaktan kar-su-eşdeğeri ve sıcaklık verilerini Rio Grande havzadaki kar erimesinden oluşan tahminleri için kar erimesinden oluşan-yüzeysel akış modeli kullanmak için azalma eğrisi kar örtüsü değişiklik oluşturmak için algılanmasında kullanılmıştır.

Özellikle kar örtüsü haritalarını eşlemek amacı için uzaktan algılama genel olarak dağlık bölgelerde çok başarılı olur. Bu çok yoğun orman örtüsü olan bölgelerde engellenmektedir.

Yeni modeller aynı zamanda kar hidrolojisi tahminleri geliştirecek uzaktan algılama verilerini kullanmak üzere geliştirilmiştir. Ayrıca, sayısal yükseklik modellemesi ve coğrafi bilgi sistemleri ile uzaktan algılama verilerinin birleştirilmesi nesnel ve sistematik olarak birleştirilecek verilerin farklı türlerini olanaklı kılar (Engman ve Gurney, 1991). Sayısal yükseklik modellemesi güneş ve güneşin geliş eğimi, bakı ve arazinin yükseltisini kullanarak görüntüleri normalleştirmek için kullanılır (Baumgartner, 1988; Miller ve diğerleri, 1982). Coğrafi bilgi sistemleri uydu görüntüleri ile bitki örtüsü maskelerinin birleştirmesine yardımcıdır (Keller, 1987).

Akım yönlendirme

Yüzeysel akış baş su bölgesinden olan çeşitli istasyonlarda konfigürasyonunu değiştirmek, sel yönlendirmesi olarak bilinen bir tekniği ile hesaplanabilir bir dalga olarak aşağı doğru hareket eder. Depolama ve diğer etkileri dalga zayıflatma eğilimindedir. Kanal koşullarında ve kollarından girişlerinin düzensizlikler problemin doğasında karmaşıklık vardır. Rezervuar ve kanallardan taşkın dalgalarının yönlendirmesi birçok yöntemler ile gerçekleştirilir.

Hidrodinamik yöntemler

Hidrolojik araştırma doğadaki su döngüsünü oluşturan fiziksel işlemler konusunda çok bilgi kazanmıştır. Benzer şekilde, modern bilgisayarlar ile birlikte zaman ve mekan içinde sürekli verilerin toplama ve entegrasyonu istihdam edilen yüksek teknoloji, her türlü hidrolojik ve meteorolojik verilerin hızlı bir şekilde işlenmesine izin verir. Bütün bunların modellenmesi, hidrodinamik modelleme üçüncü bir türünün geliştirilmesine yardımcı oldu.

Hidrodinamik modellerin havzadaki fiziksel süreçleri tanımlamak ve kütle korunumu bakımından momentum denklemlerinin sayısal entegrasyonuna dayanmaktadır. Hidrodinamik model süreçlerini yöneten fizik yasalarına dayalı olduğundan kalibrasyon aralığı ötesinde, verilere dayalı tahminler daha güvenli olan kavramsal modellere göre yapılabilmektedir. Akış ivmelenme etkileri ve su yüzeyi eğim hesaplarının tam dinamik yönlendirmesi, aşağıdaki kararsız akım durumlarında akışı ve su yüzey konumlarını doğru bir şekilde belirleyebilirsiniz:

(a) Ters yönde yukarı akım hareketi, aynı derecede bu gelgit hareketi ya da deniz-fırtına dalgalanmaları tarafından üretilen dalgalar;

(b) Aşağı rezervuar veya akarsu kolu girişleri tarafından üretilen geriye kabarma etkileri;

(c) Düz alt yamaçlarında bulunan akarsularda meydana gelen sel dalgaları: yüzde 0.05 'den az;

(d) Kontrol altına alınmış bir rezervuardan bırakılma veya bir barajın olağanüstü durum hatasından dolayı ani dalgalar.

Dinamik yönlendirme genellikle Saint Venant denklemleri olarak bilinen kararsız akışı tek boyutlu hidrodinamik denklemlere dayanmaktadır. Bu denklem, genellikle aşağıdaki öğeleri tutucu bir biçiminde ifade etmiştir.

Süreklilik:

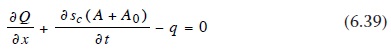
İvmelenme:

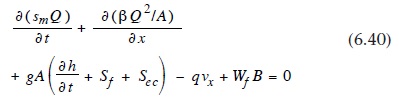
İçinde:

Burada Q akıntı olup, A etkin kesit alanı, A0 etkin olmayan veya ölü depolama kesit alanı olduğunu, Sm bir derinlik tartılır kıvrımlılık katsayısı, Sec genleşme-büzülme eğimi, β momentum kesiti içinde homojen olmayan hız dağılımı için katsayısıdır, WfB su yüzeyinde rüzgar direnci etkisi, h su yüzeyinin yükselmesi ise, VX nehir x-yönünde yanal girişin hızı olduğunu, B etkin kesit alanı üst genişliği, n Manning pürüzlülüğünün katsayısı, R hidrolik yarıçap olduğunu; olarak öncekilerin dışında diğer semboller tanımlanmıştır:

Burada Kec genişleme ve daralma katsayısı, (Q/A)2 bir x mesafe ile ayrılmış iki komşu kesitler de (Q/A)2 dönemde farkı temsil etmektedir.

Eşitlikler 6.39 ve 6.41 tam doğrusal olmadığını tespit etmek için analitik olmayan çözümler mevcuttur. Doğal nehirler için söz konusu denklemleri çözümü için sayısal teknikler iki ana kategoride sınıflandırılabilir: yöntemi günümüzde yaygın olarak kullanılır değil, özellikleri ve çok yaygın olan açık ve kapalı şemaları, sonlu fark yöntemleri. Sonlu fark yöntemleri, cebirsel denklem takımı içine kısmi diferansiyel denklemler 6.39 ve 6.40 kümesi dönüştürmek. Kesin yöntemler cebirsel denklemleri belirlenen zaman için tüm nehir kolu boyunca çözerken dolaylı yöntemler aynı cebirsel denklemleri her bir enine kesit ve nehir kolu boyunca belirlenen zamanda her bir hesap noktası için sırayla çözer.

Çeşitli çözüm yöntemleri için avantajları ve dezavantajları vardır. Sayısal istikrar ve yakınsama, gerekli bilgisayar destekli zaman ve bilgisayar depolama ve programlama ve matematiksel karmaşıklık derecesi gibi faktörler dikkate alınmalıdır. Oların daha öncesinde 6.39 ve 6.40 denklemlerinde uygulanabilecek kısmı çözüm yöntemleri şeklinde değişiklikler gerektirir.

Genel olarak, dolaylı sonlu farklar tekniği daha karmaşıktır ama birkaç gün süren kararsız akımlar hesaplarken kesin yöntemlerden daha etkilidir. Çok daha geniş zaman adımları dolaylı yöntemleri ile kullanılabilir. Açık yöntemleri basit; ancak, zaman adımları düzgün işaretlenmediği sürece onlar, sayısal kararlılık sorunlarıyla karşı karşıyadır. Bu ve diğer sınırlamalar iyice belli bir çözüm tekniği dinamik yönlendirme tahmin yöntemi geliştirmek veya özel bir uygulama için mevcut bir dinamik yönlendirme tekniğini seçeneğini seçmeden önce anlaşılmalıdır.

Dinamik yönlendirme için gerçek bir tahmin durumu uygulama içinde önemli bir görev Sf pürüzlülük parametresinde belirlenmesi olduğunu, sürtünme-eğim 6.40 denklemle verilir. Pürüzlülük parametresi çoğunlukla akış veya yükselmesi yanı sıra nehir boyunca mesafe ile değişiklik gösterir. Akış ve mesafesi deneme yanılma yolu ile birlikte pürüzlülük parametresi ilişkisinin bir öncesinde tespiti çok zaman alıcıdır. Otomatik olarak büyük ölçüde ilişkiyi belirleyen teknikler bir tahmin ortamında dinamik yönlendirmenin operasyonel kullanımı kolaylaştırır. Sınır ve bir çalışma modunda Saint Venant denklemlerin çözümü için başlangıç koşullarının düzgün değerlendirilmesi dinamik bir yönlendirme tekniklerinin uygulanmasında yeni bir kritik görevdir.

Başka bir kritik görev bütünsel hesaplama öğesi ile birlikte bütünleşmiş bağlantılı verimli bir veri toplama ve yönetim programı olarak tanımlanmıştır. Kesit geometrisi dinamik yönlendirme program tarafından kullanmak için verimli bir şekilde mümkün olduğunca işlenmiş olmalıdır. Beklenen akış koşulları için operasyonel bir tahmin aracı olarak kullanılmasının uygulanabilir olması dinamik bir yönlendirme tekniğinin mümkün olduğunca az zorunlu veri girişi istemeniz gerekir.

Biraz daha momentum denkleminin yeniden yazılması ve yanal girişlerinde meydana gelen bir ivmelenmeyi görmezden gelerek ve çok net bir görüntüyle dinamik, difüzyon ve yönlendirme kinematiği arasındaki temel farklılıkları göstererek elde edilebilmektedir.

Göz önünde bulundurun:

Yaklaşım ilk düzeyinde giriş zamanı değişimi ve hızının konumsal değişimi ile ilgili ivmelerini temsil eden koşulları ihmal edilir. Ortaya çıkan model difüzyon modeli olarak adlandırılır. Bazı akış durumlarda, ayrıca basınç kuvvetini süreli ihmal etmek yerçekimi ve sürtünme kuvvetleri arasında bir denge olarak ve momentum denklemi ele almak mümkündür. Bu yaklaşım kinematik model olarak bilinir.

Her iki kinematik ve difüzyon yaklaşımları da karadan yaklaşık yüzde 0.1 daha büyük olduğu yamaçlarda akarsu akışı ve akışlarını tanımlamak için kullanılmıştır. Difüzyon modeli küçük eğimli nehirleri üzerinde kullanılabilir ama ihtiyatlı bir şekilde kullanılmalıdır çünkü eylemsizlik bakımından önemli olabilir. Kinematik modeli nerede düzensiz geometri ve doğal havzalar topografya bir dizi akışı düzlemleri ve düzenli kanal parçaları gibi basit öğeler tarafından değiştirilebilir uygulamalarda daha popüler hale geldi. Kinematik denklemlerde kirleticilerin taşımasının tahmini su kalitesi modellerinde de kullanılır. Bir kinematik modeli karşısında etkilerinden yanal girişlerinde veya aşağı rezervuar durgunluk etkilerini dikkate almaz, o memba yönünde dalga ilerlemelerini tahmin etmek etmek için kullanılabilir.

Hidrolojik yöntemler

Sadece süreklilik denklemi veya kütle korunumu yasasısıla hidrolojik sel yönlendirme yöntemlerini kullanın. Bu teknikler, sadece dalga yayılması artışları ve azaltır depolama için iki ölçüm noktaları arasında uzanan erişilmesi kolay olduğunu bir durumu göz önünde bulundurarak incelenmiştir. Ancak, depolama ve akış arasındaki ilişkileri bu yöntemlerle deneysel olarak belirlenir, çünkü onlar akış verileri ve düzeyleri tasarım amaçları için gerekli olduğunda doğrudan kullanılamaz.

Hidrolojik yönlendirme yöntemleri istihdam edilmektedir, akış yukarı bir noktada verilen ya da üstlenilen ve yönlendirme akışı ve akış noktası aşamasını hesaplamak için kullanılır. Yönlendirme, depolama ve akışı arasındaki ilişkiyi kullanarak aşağıdaki süreklilik denklemi bir çözüm oluşmaktadır:

I – Q = dS/dt (6.44)

Burada I ve Q sırasıyla, üst ve alt noktada deşarjları olup, S nehir depolama ve aşağı kesitlerde akış yukarı arasında erişme uzaklığı ve t zamanı. Bu denklemin çözümü hidrolojik akım ana güçlük yönlendirme depolama-akım ilişkisini yaklaşımları içerir. Ancak, yeterli hidrometrik veri ile bu ilişkileri deneysel olarak elde edilebilir.

Basit yönlendirme yöntemlerinin analitik çözümlerini, doğrusal depolama–akım ilişkileri temel olarak ele etmek mümkündür. İki tür yöntemleride aşağıda gösterildiği gibi kısa mesafeli tahmin uygulaması içinde geçerlidir.

(a) Muskingum yöntemi, aşağıdakilerden hangisi depolama-akım ilişkileri üzerine kuruludur:

S = K [xQ1 + (1 – x)Q2] (6.45)

Sabitler K ve x akıntı verileri belirli bir erişim için deneysel olarak elde edilmiştir. Onlar x in çeşitli değerleri için S ‘e karşılık xI+(1 – x)Q çizimleriyle tespit edilebilir. X ‘in en yakın değer verilerin sonuçları tek bir değer eğrisi için en yakın çiziminin bu olduğudur.

Muskingum yöntemi genellikle aşağıdaki farklı biçimde kullanılır:

Qj+1 = C1 Ij+1 + C2 Ij + C3 Qj (6.46)

Burada C1, C2 ve C3, Muskingum parametre olan fonksiyonları K ve x ve zaman adımı t, toplamı sağlayan birim için sabitler toplamı birliğinin eşit olduğunu;

(b) Belirli erişim yöntemi, Kalinin ve Miljukov (1958), tarafından önerilen aşağıdaki doğrusal depolama-akım ilişkisi üzerine kuruludur:

Q = K S (6.47)

Burada K depolama sabit erişim yoluyla seyahat süresine eşittir. Yukarıdaki denklem geçiş bölgelerinde belirli süreye ulaştığında geçerlidir, L bu eşitlik kabaca:

Burada Z su yüzeyi eğimi olduğunu ve Q/h bir seviye-boşaltma ilişkisinin tanjantı. Bir nehir kademesi birkaç belirli bölgelerinde oluşuyorsa, yönlendirme art arda gelen bir belirli erişim aşağı gelecek şekilde gerçekleştiriliyor. Birincil ulaşabileceği akım noktası için hesaplanmış olan boşatma miktarı ikinci erişim noktası ve diğerleri için giriş olarak kabul edilmektedir.

Akış tarafından aynı doğrusal bir rezervuar sistemi ile akım dönüşümünü ifade eden aşağıdaki formülde uzunluğun belirli bölgelerinde sayısını belirlemek için gereken verilerin eksikliği durumunda akarsuyun uzunluğu ulaştığı için aşağıdaki formül kullanılabilir:

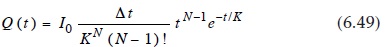
Burada N karakteristiği ulaştığında veya rezervuarlarının sayısını, K bir karakteristik erişim için yolculuk zamanı, I0 birinci karakteristiği erişim içine girişi olduğunu ve t zamanı. K ve N parametreleri deneme yanılma yoluyla veya en uygun şekle sokma/optimizasyonu tarafından belirlenir.

Rezervuar yönlendirme

Bir rezervuar pik debi azalmasına neden olur, bu bir rezervuar aracılığıyla sel geçişi ile bir kanaldan geçit arasında oldukça farklılık gösterir, çünkü bir yerde rezervuar olmasaydı oluşacak miktar ile karşılaştırıldığında en yüksek boşaltma/azalmaya yol açaracaktı.

Bir rezervuar sel dalgası hızı kanalları daha yüksek olduğundan, en yüksek çıkış ile en yüksek girişe göre gecikme mutlaka rezervuar inşaatından önceki hakim koşullarda ortaya çıkan zirveye göre gecikme anlamına gelmiyor. Ayrıca, rezervuar inşaatı kimi zaman pik deşarj azaltılmasında etkisi olmasına rağmen, aşağı akım taşkın koşulları daha da kötüye gidebilir. Zayıflatılmış zirveye çıkış aşaması genelde belli kollarıdaki zirve safhası ile ortaya çıkabilir. Böylece, rezervuarın yapımı aşağı akım taşkın koşullarını artıracağını hafife alınmaması gerekir. Hidroloji ve tasarım koşullarında geçerli olacaktır hidrolik dikkatli bir şekilde incelenmelidir.

Baraj kesmeleri

Bir baraj başarısız olduğunda, ani gelen sel sonucunda baraj çıkışında aşım ihlali olacağından barajın altındaki vadide sel basmaları felaketi oluşur. Örneğin, buz reçeli ya da moloz akımı için insan yapımı bir baraj başarısız olabilir. Genellikle baraj kesmesi çıkışının bazı kere ilgili nehir üzerinde herhangi bir önceki taşkından daha büyüktür. Yapay ya da doğal barajların başarısızlığı modlarıyla ilgili az şey bilinmektedir. Dolayısıyla, sellerin gerçek zamanlı tahmini barajı-kesmesinde barajın başarısızlığı gerçekten gözlenmiştir, baraj başarısızlığı neredeyse daima sınırlıdır. Planlama hesaplamaları için kabul edilebilir farklı hasar tipleri, aşağı akım gelişimine etkileri imar ya da tahliye durum planları açısından incelenmiştir.

Bu sorunu daha eski klasik çalışmalarda ani baraj yıkılması ve idealize edilmiş aşağı akım koşullarında varsaydım. Son zamanlarda, mühendisler Schocklitsch ya da benzeri maksimum akım denklemine dayalı bir üçgen şeklindeki çıkışının hidrografı varsayımı ile soruna yaklaşmaya çalışmışlardır:

Burada g yerçekimi ivmesi olduğunu, Wd ihlalin genişliğidir ve Y0 baraj arkasındaki suyun yüksekliğidir. Denklem 6.49 ve deneysel/ampirik bir durgunluk katsayısı kullanılarak sentezlenmiş hidrografın bir hidrolojik yönlendirme tekniği ile aşağı akım vadisi üzerinden yönlendirilir. Alternatif olarak, daha gerçekçi bir yaklaşım içinde dinamik yönlendirme teknikleri (bkz: 6.3.4.2) güzergahı hızla değişen ve nispeten büyük baraj-kesmesi taşkın dalgası için ulaşılabilir. Aşağı akım barajlarda hesabında açıkça, set üstü depolama, aşağı akım otoyol bentleri, genişleme ve daralma kayıpları dikkate alınmaktadır.

Zaman, bir baraj kesmesi taşkının gerçek zamanlı tahmininde önemli olduğu için, operasyonel tekniklerini hesaplama süresinin verimli olması gerekir. Bununla birlikte çok daha önemlisi dikkate alınması için tahmin tekniğinin verileri gerekliliktir. Dinamik yönlendirme için tüm veri ve tahmin yönlendirme aşamasında gerekli kesit veri miktarını en aza indirmek için her türlü çaba yapılmalıdır ve program dosyaları hemen kullanıma hazır halde olması gerekir.

Diğer süreçler modelleme

Sediment taşınması modellemesi

Sediment taşınım modelleri, katı madde taşınımı oranı ve su yüzeyi yüksekliği veya hidrodinamik model kullanılarak belirlenen hızlarının temel yönünü tahmin etmek (bkz. 6.3.4.2), sürekliliği ve momentumu Saint Venant denklemlerin sayısal çözümüne dayalı katı madde taşınımı modelinin önemli bir parçasıdır.

Temel katı madde taşınımı süreçleri erozyon, sürüklenme, taşıma ve biriktirme şeklinde bölünmüş olabilir. Dere yatağı üzerinde sediment sadece akış alanındaki enerji kuvvetlerinin etki ettiği sürece erozyon için kritiktir, kayma gerilimi eşik değerin altında kalması ile hareketsiz bir şekilde kalacaktır. Kritik bir kayma gerilimine ulaşıldıktan sonra, sedimentler sıçrama ya da zıplatma, yuvarlanma ve kaydırma biçimlerinde hareket etmeye başlar. Bu hareket, yatak yükü olarak bilinir. Çeşitli araştırmacılar tabanında kayma gerilmesi bir fonksiyonu ve tane çapı olarak bu yatak yükünü açıklayan ilişkiler geliştirmişlerdir. Bu katı madde taşınımı fonksiyonları olarak bilinen ve daha çok birleşmeyen malzeme için geçerlidir (bakınız, 4.8.6).

Parçacık-çökelim hızı hesaplanması bazı birleşmeyen katı madde taşınımı fonksiyonları için gereklidir.

Burada:

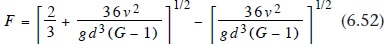
d çapı 1 mm ile 0.0625 mm arasındaki parçacıklar için. 1 mm den fazla parçacıklar için, F = 0.79. Yukarıdaki denklemlerde, f çökellerin düşüş hızı, g yerçekimi ivmesi olduğunu, G çökellerin biyojeokimyasal özgül ağırlığı ve v suyun kinematik viskozitesidir.

Tortu ve akış koşulların tümü için doğru bir şekilde uygulanabilecek evrensel bir işlevi yoktur çünkü sediment taşıma modellerin çoğu, birden fazla işlevin kullanılmasına izin verin. Bu taşıma işlevlerin çoğu boyut fraksiyonu tarafından yükü aşağı kesmeden toplam yatak yükünü hesaplamak için geliştirilmiştir. Bazı taşıma modelleri yatak yükünü tane boyutu dağıtımının değişim hesabını farklı boyut fraksiyonları için bu işlevleri geçerlidir ve yapabilirsiniz, yatak malzemesi karıştırma süreçleri ve bu nedenle kaplama tabakaları etkilerini simülasyonu yapabilirsiniz.

Taşımacılığı, sedimentin toplu askı halinde nakli olarak karakterize edilebilir. Asılı yük hesapları yerel hidrolik koşullarındaki değişiklikler için katı madde taşınımına cevap olarak zaman mekan gecikmesi şunlardır. Tabanındaki kayma gerilmesi birikimi için kritik değeri aşıyor olarak taşınmasında korezyonlu sedimentler uzun süre askıda kalacaktır. Korozyonlu sedimentler düşük yoğunluklu birimleri güçlü sediment türüne bağımlı bir süreci ayrım eğilimindedirler, su ve akış koşullarında iyonların konsantrasyonu ve artık parçacık boyutu çökelme hızının bir fonksiyonudur. Bu kümeleme çöktürme hızlarını atamak suretiyle modellerinde hesaplanmıştır. Genel olarak, eşzamanlı birikimi ve kaynaşmış çökellerin erozyonu olarak meydana gelmez, fakat kaynaşmış sediment yatak yapısında zamanla ve örtü tabakası ile birlikte değişiklikler bulunmamıştır.

Erozyon hızı biriktirme oranı farklı olmadığı sürece yatak yükselmesine net değişimde hiçbir değişiklik olmaz; Bunun sürekli ve bağımsız olarak devamının iki süreci bulunmaktadır. Yatak seviye değişimi bir sediment süreklilik denklemi ile belirlenebilir. Denklem asılı sedimentin hacim değişiklikleri çok genel olarak uzun vadeli kararlı akış simülasyonu için de geçerlidir, yatak sediment hacmi değişiklikleri daha küçük olduğu varsayımına dayandırılarak türetilmiştir. Sediment için kütle korunumu denklemi azaltır:

Burada   bir birim yatak tabakası hacmindeki sedimentin hacmi (eksi bir gözeneklilik), Ad birim uzunluktaki yatak sediment hacimdir, Qs hacimsel sediment deşarjı ve qs birim uzunluktaki yanal sediment girişinin olduğunu.

Belirli sediment taşıma ve morfolojik modelleri, öyle aynı derecede MIKE 21C gibi sırayla kesişme noktası oyulması, oyulma viraj gelişimi ve noktası çubuklarının oluşumu gibi alternatif çubukları simüle etmek için katı madde taşınımı simülasyonları ile birlikte her bir sel akım bağlantısını göz önünde alın. Bu modellerde eğrisel hesaplamalı ızgaralarırı/gridleri sağlayabiliyorsanız nehir morfoloji modelleme için daha çok uygundur. Set aşınması her biri işlemsel zaman aşamasında dahil edilmiştir. Erozyona uğramış set malzemesi sediment süreklilik denkleminin çözümüne dahil edilmiştir. Set erozyonu uyarlanabilir eğrisel bir ızgara hareketi ile modellenmiş bir geri çekilen set hattı üretecektir.

Sediment modelleme hakkında ek bilgi 4.8.6 bulunmaktadırr.

Su kalitesi modellemesi

Doğal ve yapay su kaynaklarına su kalite yönetimi, çeşitli yönetim alternatifleri açısından su kalitesi özelliklerinin izlenmesini gerektiren kompleks bir görevin etken faktörleri ve bu özelliklerin gelecekteki değişikliklerin öngörülmesi ile ilgili olarak izlenen verilerin yorumlanması aşamasında da dikkate alınır. Bu sorunların çözümü büyük ölçüde su kalitesi modelleri kullanımı ile destekli olabilir.

Bu aşağıdaki faktörler temelinde tahminini sağlar:

(a) Kirlilik girişleri üzerine giriş verilerinin bir serisi;

(b) Meteorolojik-çevresel başlangıç koşulları;

(c) Hidrolik-hidrolojik ve su kütlesi ve havza arazi kullanım özellikleri;

(d) Zaman ve/veya mekan içinde çeşitli su yönetim alternatifleri için düşünülen su kütlesinin bazı su kalite özelliklerinin gelişimi.

Su kalitesi modelleri sıklıkla hidrolik ve hidrolojik modeller ile bağlantılıdır.

Matematiksel su kalitesi modelleri, genel kademelerine göre sınıflandırması yapılır (bkz: 6.1) ve aşağıdaki ölçütlere göre sınıflandırılabilir:

(a) Su kalitesi bileşenleri: Tek veya çok bileşenli modelleri halinde;

(b) Modellenmiş bileşenli türü: muhafazakar, örneğin, tuz; muhafazakar olmayan fiziksel, örneğin, sıcaklık; muhafazakar olmayan kimyasal, örneğin, oksijen dağılımı; ya da muhafazakar olmayan biyolojik, örneğin, koliform bakteriler.

Nehirlerde kirlilik taşıma açıklaması için, uygulamada en çok kullanılan model adveksiyon-dispersiyon denkleminin dayanan tek boyutlu modeldir:

Burada C kirletici konsantrasyonu olduğu için, u ortalama suyun hızı, D boyuna dispersiyon katsayısı, t zaman ve x mesafedir.

Uzunlamasına dispersiyon katsayısı Fisher denkleminin esas alınmasıyla hesaplanır:

Burada u'2 içinde kesitsel ortalamadan sapma, l en uzak set için maksimum hız boyunca olan uzaklıktır ve z enine karıştırma katsayısıdır.

Bir nehirde kirletici taşımada bu modeli uygulamak için, her birkaç kilometre uzunluğunda, nehir ulaşımı içinde su hızı sabit olduğu kabul edilecek şekilde ayrılmıştır. Her bir sektörün içerisinde su hızı bir hidrolik ya da hidrolojik model (6.3.4 bakınız) olarak hesaplanır. Su kalitesi modelleri mekan ve zaman içinde su kalitesi izleme ağlarının tasarımı da dahil olmak üzere birçok amaç için su kalite yönetimi olarak kullanılabilir su kalitesini belirleyici faktörleri ile ilgili olarak elde edilen verilerin yorumlanması, diğer çevresel (hava, toprak) ile birlikte kirlilik arabirim modelleri ve ekolojik modelleri ile birlikte veya çeşitli alternatif kirlilik düzeltme önlemleri olmaksızın su kalitesi eğilimlerin değerlendirilmesi ve bir kirleticinin ve variş zamani boyunca nehirdeki bir konsantrasyon profilinin değerlendirilmesi.

Su kalite modelleri, pek çok ülkede (Biswas, 1981) su kalitesi yönetimi sorunların çözümü için değişik derecelerde başarı ile uygulandı. Örneğin, nispeten basit bir model Büyük Britanya ve Kuzey İrlanda Birleşik Krallığındaki Thames nehri içine Severn nehrinden itibaren büyük ölçekli su transferleri su kalitesi üzerinde etkilerini araştırmak için kullanıldı. Modeli üzerinde yoğunlaşması muhafazakar ve neredeyse koruyucu maddelerin suda bulunan çok sayıdaki bu türden transferlerin etkisini değerlendirmek için kullanıldı. Modelin kaynağına göre nehrin akışının ayrılmasına dayanan, örneğin, yüzey, arayüz ve baz akımı ve her bir kaynak için kabul edilen belirleyicilerin konsantrasyonları ve su girişleri ve giriş varyasyonları arasında gelişen ilişkiler üzerine kuruludur. Simülasyon sonuçları gayet iyi kaydedilmiş verileri eşleştirdi.

Su yönetimi amaçları için bir su kalitesi modelinin pratik uygulamanın bir başka örneği Ontario, Kanada Thames nehrinin su içinde çözünmüş oksijen konsantrasyonu üzerine atıksu arıtma tesisi ile biyokimyasal talep yüklerinin giderim etkisinin çalışmasıdır. Sonuç kriterleri üzerinde elde çözünmüş oksijen konsantrasyonları başka bir noktada bu çok güç olacağından, biyokimyasal talep yüklerini kaldırmak bir noktada uygulanabilir olduğuna göre iyi su kalitesi için kabul edildiğini göstermektedir. Su Kütlelerinin Yanlışlıkla Kirletilmesinin Hidrolojik Özellikleri (WMO-No. 754) önemli kirlilik sorunları olan çeşitli nehirler olarak Kanada, Fransa, Almanya, Polonya, İngiltere ve Amerika Birleşik Devletleri'nde uygulanan su kalitesi modelleri, çok sayıda ayrıntılı bir inceleme sunuyor.

Su kalitesi modelleri de kaza sonucu kirlenme olaylarında yayılmanın hesaplaması için kullanılır. Bu tür modeller 1989 yılından beri Ren nehri üzerine operasyonel hale getirilmiştir. Öncelikle yukarıda bahsedilen modellerin çoğu belediye ve endüstriyel atıkların kaynaklanan kirleticiler düşünülür ise bazı da ormancılık ve tarım faaliyetleri veya kanalizasyonsuz konutlar gibi yaygın kaynaklardan oluşturulmuş kirliliği düşünmek gerekir.

En yaygın olarak kullanılan modeller arasında toprak ve su için değerlendirme aracı anlamında SWAT dir. Besin maddeleri ve böcek ilaçları gibi tarımda yaygın olarak kullanılmasıyla bu kaynaklardan gelen suya geçme kaderinin simülasyonunu sağlar. SWAT Arnold ve ortakları tarafından geliştirilen arazi yönetimi uygulamalarının su, tortu ve tarımsal kimyasal verimleri etkilerini tahmin etmek için ABD Tarım Bakanlığı (USDA) tarımsal araştırma hizmeti için geliştirilen havza ölçeğinde bir modeldir (Arnold ve diğerleri, 1993). Modeli hem yarı deneye dayalı ve fiziksel nitelikteki önemli unsurları birleştiren bir süreç tabanlı model olarak adlandırılabilir. Bu nedenle, hava durumu hakkında bilgi, toprak özellikleri, topografya, bitki örtüsü ve havzada meydana gelen toprak yönetimi uygulamalarını gerektirir. Su hareketi, sediment hareketi, bitki gelişimi, besin maddeleri ve döngüleri gibi ilişkili fiziksel işlemlerde doğrudan bu giriş verilerini kullanılarak SWAT tarafından modellenmiştir. SWAT sürekli bir zaman modeli için tasarlanmış değildir, saatlik zaman adımları ile sel gibi detay tek olaylarda simüle etmek için tasarlanmıştır.

SWAT’ın hedefi makul doğruluğu düşünülen secilmis bir nehir havzasınde su, sediment, besin ve ilaç verimleri üzerine yönetim kararlarının etkisini tahmin etmektir. Model aşağıdaki bileşenleri içerir: hava, yüzeysel akış, dönüş akımı, sızma, buharlaşma, iletim kayıpları, Su birikintisi ve rezervuar depolama, bitki büyümesi ve sulama, yeraltı suyu akışı, besin ve ilaç yüklemesi ve su transferi. Model için Windows (Visual Basic) te geliştirilen, GRASS ve ArcView arabirimler geliştirilmiştir. SWAT da geniş ölçüde doğrulama gerçekleştirdi. Daha fazla bilgi için bkz: http://www.brc.tamus.edu/swat.

İzleme modeller bir dizi SWAT üzerinde dayanmaktadır. Örneğin, toprak ve su entegre edilmiş model anlamına SWIM, orta ölçekli ve geniş bir akarsu havzalarında iklim ve arazi kullanımı değişikliği etkisinin değerlendirmesi için özel olarak ve bölgesel ölçekte (1998, 2000) Krysanova ve diğerleri tarafından geliştirilmiştir. O hidrotopiler ve çeşitli değiştirilmiş rutinleri örneğin, nehir yönlendirmesini ve ormanı modülleri ve yeni yordamları için ürün oluşturucu, iklim verileri enterpolasyonu, fotosentez ve terleme daha yüksek CO2, besin saklama ve karbon döngüsü modülü düzeltilmesi gibi etki çalışmaları üç aşamalı şekilde ayrıştırma düzeni içerir. Akifer sistemlerinde kimyasal madde hareketini çoğaltmak çok sayıda modelleri vardır. Bazıları, belirli bir durum için ısmarlama çalışır ve diğerleri MODFLOW ile MT3D bağlantı akışı modelleriyle bağlantılıdır.

Yeraltı suyu durumunda, su kalitesi modellemesi akiferdeki akış rejimi anlayışına bağlıdır. Böylece, yeraltı suyu akışı oranları ve yönünü ve bunların değişkenliğinin bilinmediği sürece nokta modeli karmaşık kimyasal değişikliklerin akiferdeki girişi sırasında küçük bir nokta bulumaktadır. Ancak, kimyasal madde anlayışı ile akiferin ve kimyasal maddelerin, hem doğal antropojenik dağılımı içerisinde iş süreçleri ile önemli anlayışlar akiferin içindeki akış sürecinde elde edilebilir. Böylece iki süreç genel olarak kalibrasyon yardımıyla birlikte kullanılabilmektedir.

Buz yapısı modellemesi

Bir nehrinde buz oluşumu su yüzeyindeki tabakasında sıcaklık 0°C altına doğru soğuduğunda başlar. Akış yüzeyinin altında suyun sıcaklığı o zaman genellikle 0 °C üzerinde kalır. Böylece, buz görünüm tarihindeki tahmini suyun yüzey tabakasının 0 °C için soğuması ile bu sayede suyun yüzeyinde ısı alışverişi işlemiyle oluşmaktadır.

Su sıcaklığı tahmini, ısı kaybını etkileyen değişkenleri dikkate alırken, ısı-bütçe denklemi kademeli bir çözümü tarafından gerçekleştirilmelidir. Su yüzeyinden ısı kaybı, hava sıcaklığı, rüzgar hız ve su türbülansının bir fonksiyonudur. En genel biçimiyle, belirli bir zaman aralığı için hava-su arası ısı dengesi denklemi aşağıdaki gibidir:

Burada akarsuyun su kütlesinin ortalama sıcaklığı, su yüzey sıcaklığı (°K) olduğunu, α hava-su arayüzü su kütlesi ısı transferi (Watt/m2 °K) katsayısı ve Q Watt/m2 su yüzeyinden ısı kaybıdır.

Nehirlerin üzerinde buzun ilk olay tarihini takip modern kısa vadeli tahminlerin temelini Hydrometeoizdat (1989) tarafından geliştirilen bir yöntemdir. Bu yöntem iki ısı akısı arasındaki eşitsizlik üzerine kuruludur:

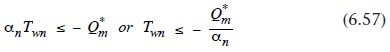
Burada Tw su akışı ortalama sıcaklığı, αn su kütlesinin ısı verim katsayısı, Qm* hava-su arayüzünden ısı kaybı ve n bu eşitsizliğin görünen süresi anlamına gelir. Tw , αn, Qm* hesaplanması çeşitli meteorolojik ve hidrolojik değişkenlerin bilgisini gerektirir. Hava sıcaklığı tahminleri kullanılabilir birkaç gün öncesinden varsa bu yöntem kullanılabilir. Doğru çalışması öngörülen hava sıcaklığı hatalarından çoğunlukla etkilenmektedir.

Donma başlangıcı için gerekli durum, buz kütlelerinin birleşmesi akan su tarafından uygulanan kuvvetin etkisi nedeniyle direnir, böylece yoğun ısı kaybı ile yüzen buzul kütlesindeki yeterli miktardaki birikimidir. Bu durumu aşağıdaki deneysel formül ile ifade edilir:

Burada (Qa)c kritiktir, donma gününde veya olabilecek en yüksek ortalama günlük hava sıcaklığı, v ulaşma akışınnın ortalama hızı, b nehir genişliği ve Qa toplamı buzul görünümünün ilk günden itibaren günlük sıcaklıkların ortalamasıdır (Buzin ve diğerleri, 1989). Günlük ortalama hava sıcaklığı kritik noktasının (Qa)c altına düşene kadar tahmini ile yapılan hesaplamalarda, her gün için arka arkaya günlük ortalama sıcaklıklar olarak denklem 6.55 olarak hesaplandı.

Operasyonel Uygulamada, buz modelinin tam sürümünü genel olarak kullanılmaz, özel konumu ve hidrometeorolojik verilerle ilgili güncellemelerin basitleştirilmiş bir çeşidi de dahil olmak üzere oluşumu kapsamaktadır. Kural olarak, model geliştirme ve uygulama kullanıcı gereksinimlerini karşılamak üzere özel olarak hazırlanmıştır. Böylece, su-yönetimi planları kış koşullarında çalışması uygun raporlar ve tahminler üzerinde dayanmalıdır. Tahmin gereksinimlerine göre işleyebilir bir buzul odaklı hidrolojik ağ, bu esaslara göre uygulanması gerekmektedir.

Su yöneticilerinden düzenli geribildirimler tahmin merkezi için de gereklidir. Hidroelektrik üretimi için bu yoğun yüzer buz kristali ve çamur üretiminin başlangıç tahminleri olması önemlidir. Teorik yöntemin basitleştirilmiş bir türüne dayanan deneysel formüller genel olarak bu amaç için geliştirilmiştir. Genel olarak, deneysel oranları nomogramlar olarak temsil edilir, bir örneği şekil II.6.16 verilmiştir.

Kısa süreli buz olayların tahmin ilişkileri buz (Hydrometeoizdat, 1989) oluşumu için gerekli koşulları olarak varolan fiziksel ya da istatistiksel bilgiye dayanır. Bu ilişkilerin fiziksel yorumu, doğal göllerde su kütlesinin soğutulmasını yöneten süreçleri ile ilgili teoriler üzerine kuruludur. Bu denklemlerin kritik bir eşik veya hava sıcaklığını veya aşılması negatif hava sıcaklıkları, bir su kütlesi üzerinde buz örtüsü oluşumunda sonuçların toplamını belirlemek için kullanılır. Bir rezervuarın donma noktasının koşulları su kütlesinin ısı içeriğine bağlı olarak, kritik hava sıcaklığı su seviyesi veya akımdan elde edilen su parametreleri ile bu hava sıcaklığına bağlı olarak deneye dayalı bir oran ile belirlenir.

Buz kalınlığı modellemesi

Buzul olayı tarihini takip ve buz örtüsü oluşumu tahminlerin yanı sıra, sonbahar buz olayların tahminlerini diğer türleri de verilmektedir. Buz kalınlığı tahminleri ısı kaybı hesaplamalarına dayanır. Buzul kalınlığında artışları ağırlıklı olarak ve alt tarafında meydana gelen su sütunundaki enerjinin durumu tarafından belirlenir. Bazen buz örtüsü kalınlığının buzul yüzeyindeki kar örtüsünün erimesiyle suyun donması yüzünden üst yüzeyinden büyür. Erime suyuna genellikle yağışlar eşlik etmektedir. Bu da buzul üzerinde artan basınç nedeniyle buz örtüsü üzerinde ilaveten oluşan bir miktar suya sebep olabilir.

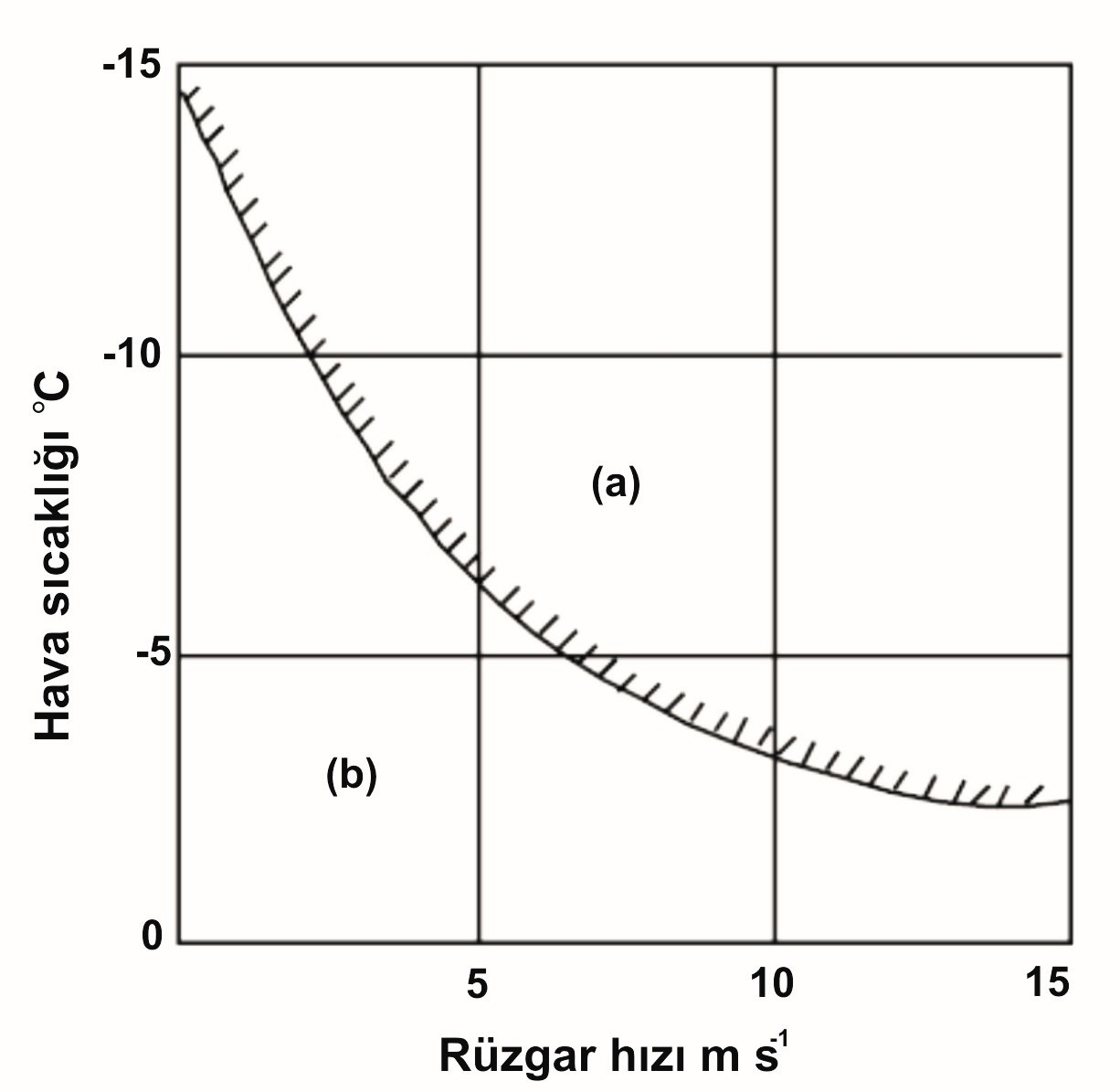
Şekil 16. buzul – yıpranma oluşumu tahmini: (a) sulu kar mümkün, (b) sulu kar yok

Buz kalınlığının tahmini buz alt yüzeyine temas eden su sütunundan ısı girişi ve ile buz yüzeyinden atmosfere ısı çıkışı arasındaki farkın tahminlerini temel alır. Isı kaybı için bir artış kalınlıkta buz derinliği sağlayacaktır:

Burada hice buzul kalınlığındaki santimetre cinsinden büyüme olduğunu, kar-buzul örtüsünün üst yüzeyinden atmosfere olan bir ısı akışını, buzun alt yüzeye ısı girişleri olduğunu, Lice buzul oluşumu özgül ısı; ve ρice buzun yoğunluğudur.

Formülleri hesaplanması ve tahminleri buz örtüsü oluşumu, çeşitli koşullar altında buzul kalınlığı için literatürde mevcuttur.

Buz parçalanma modellemesi

Buz tıkacı tarihini tahmin etmek için bir yöntem söz konusudur, nehir erişim üzerinde parçalanma için gerekli olan pozitif hava sıcaklığının kritik derece-gün toplamından tahmin edilmesi ilkesine dayanmaktadır. Parçalanma ve kış dönemi için negatif derece-gün toplamı arasındaki ilişki bu toplamın belirlemek için kullanılır. Bu yöntemle buz parçalanma tarihini tahmin etmek için birkaç gün önceden bir hava sıcaklığı tahmininin olması gerekir. Parçalanma tarihindeki derece-gün toplamını hesaplamak ve birkaç gün önce beklenen hava sıcaklıklarını kullanarak kritik değeri ile karşılaştırma yaparak elde edilir.

Buz kalınlığı azaltılması ve buz örtüsü tahmin, gerilme ve tahminleri, buz-tıkacı gelen buz depoları, nehirler ve açıklamalar için buz örtüsü imha modelleri, öyle aynı derecede Hydrometeoizdat (1989) ya da Bulatov modelleri gibi bulunılabilir modeller ile yapılır. İkincisi, genel bir denklem kullanılarak geliştirildi, nehirlerin üzerinde buz tıkacı tarihleri tahminleri on günlük bir gecikme zamani ile orta vadeli tahminlerin verilmesini sağlayan bir yöntemdir. O olabildiğince sadece seyrek veriler (Borsch ve diğerleri, 1987) ile nehirler de dahil olmak üzere, her yerde buz tıkacı tahminlerini geliştirmeyi sağlar.

Rezervuarlarda buz dağılması

Bir rezervuar sonuçları üzerinde buz örtüsü ile parçalanma yoğunluğu kademeli olarak bir düşüş ile eritilebilir. Rüzgar hareketi altında, buz içine genel bir buz kayması taşıma işlemine çeşitli boyutları ayrı buz akımlarını bozabilir. Buz sürüklenmesinin bir başlangıç koşulu aşağıdaki biçimdeki gibi bir eşitsizlik ile ifade edilir:

Burada φ  eriyen buz (göreceli eğilme gerilmesi) boyutudur, dg santimetre cinsiden buzun kalınlığı, U 24 saatlik bir süre içinde maksimum rüzgar hızı ms-1 ve C deneye dayalı olarak elde edilen rüzgar hızına bağlıdır ve belirli bir rezervuar için sabit bir katsayısıdır. Bağımsız Devletler Topluluğu ülkelerindeki bir dizi rezervuarları için, C değeri 0.018 olarak bulunmuştur. Buzun boyutu φ ve kalınlığı dg buz sürüklenmeye başladığı zaman ısı dengesi denklemleri kullanarak meteorolojik elemanlar hesaplanır. Bu yöntem hakkında detaylı bilgiler Hydrometeoizdat (1989) tarafından sağlandı.

Nehirlerde buz parçalanması

Nehir üzerinde buz parçalanmasının model bazlı tahminleri modelleri parçalanma koşulunun buz örtüsünün kalınlığı ve özelliklerine bağlı olarak buz ve mevcut sürükleme gücü ile belirlenir. Direnç kuvvetleri eşit veya çekme kuvvetinin daha az olduğu zaman, buz örtüsü parçalanmaları ile bir buz hareketliliği başlar.

Parçalanma için durumu aşağıdaki ilişki ile ifade edilir:

Burada dg, eriyen buz ve kalınlığının göreceli gerilme ürünü, parçalanma sırasında buz örtüsünün yoğunluğunun bir ölçüsüdür ve H ile H akımın çekme kuvvetini temsil eden parametrelerdir. H parçalanma sırasında suyun seviyesinin yüksekliği ve boşaltma ile akışın hızlını yansıtır ve H parçalanma zamanında yukarı yükselişi, H3 kışın minimum seviyesinin üzerindeki suyun seviyesini, sayısal olarak eşitlik H = H - H3. Çoğu zaman H ve H birbiriyle ilişkili olduğundan, bu denklemi 6.61 açıklanan ilişkisi bu miktarların sadece birininin kabulü yeterlidir. Tahmine dayalı miktar ve kırılma öncesi birkaç gün için gerçek verilere dayanmaktadır. Aşağıdaki gibi ilişkilerin bir yaklaşımı ifade edilebilir:

Buradaki a ve b deneysel katsayılarıdır.

Seçilmis nehirler hakkında buz kırılma tarihleri tahmininde veya sadece kullanılabilir gözlemlerin kısa sürelerle bulunduğu bir tahmin yöntemi, genelleştirilmiş bir denkleme dayanarak geliştirilmiştir:

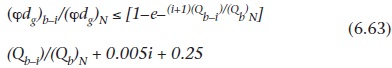
Burada (dg)N buz kırılması günü buzun ortalama göreceli dayanıklılığı olduğunu, (dg)b–i buz kırılması öncesi i gün boyunca buzun göreceli dayanıklılığı olduğunu, Qb–i buz kırılması öncesi i gün boyunca suyun deşarjı, (Qb)N buz kırılması günü ortalama deşarj olduğunu. (dg)N, (Qb)N, hesaplama ve tahmini ve dg özel olarak geliştirilmiş haritalar, nomogramlar ve tablolar kullanılarak yapılır (Borsch ve Silantjeva, 1987).

Buz-örtüsü kırılması modeli, buz kırıcılarının konuşlandırılması maksadıyla hazırlanmış tahminleri üretmek buz için maksimum izin verilen azami yüklemenin tahmini gibi bazı ilave özel amaçlı tahminlerin geliştirilmesini sağlar.